투자성과의 측정

이 블로그에서 주로 사용하고 있는 투자성과 지표들을 정리한다. 학문적인 정의와는 다소 다를 수도 있고, 필요에 의해 새로 만들어진 지표도 있음을 미리 알린다.

수익률
- CAGR
- 초과수익률
변동성
- 사후적 변동성 (ex-post volatility)
- 사전적 변동성 (ex-ante volatility)
Semi-deviation
- Downside risk
- Upside potential
추적오차
- 사후적 추적오차 (ex-post tracking error)
- 사전적 추적오차 (ex-ante tracking error)
위험조정수익률
- Sharpe
- Sortino
- IR
MDD
Beta
Hit ratio
Profit-to-loss
Consistency
Rolling stats
- Rolling stats의 중간값
- 손실 가능성

수익률

CAGR

투자성과가 첫해에는 +100%의 수익, 둘째해에는 -70%의 손실이 발생했다고 가정해보자. 평균적으로 매년 몇 %의 수익이 발생 했을까? 가장 쉽게 생각할 수 있는 건, 연 산술평균 수익률 $\frac{+100 - 70}{2} = 15$ % 일 것이다. 그렇다면 최종적으로 내 손에 쥐게 되는 금액은 얼마일까?

$100 \times (1+1) \times (1-0.7) = 60$

초기투자액이 100원이라면, 2년후 60원이 된다는 의미이다. 매년 15%를 벌었다고 생각했는데, 결국 40%의 손실이 발생하게 된 것이다. 여기에는 복리의 트릭이 숨어있다. 첫해의 투자수익 100%는 초기투자액 100원에 적용되어 내 자산은 200원으로 불게 되지만, 다음해의 투자손실 70%는 초기투자액 100원에 적용되는 것이 아니라 직전해의 200원에 적용된다. 즉 100%의 수익이 70%의 손실보다 언뜻 커보이지만, 실제 금액으로는 70%의 손실이 훨씬 큰 것이다.

따라서 산술평균 수익률은 실제 투자성과를 왜곡할 가능성이 매우 높다. 실제적으로 연수익률은 다음과 같이 계산되어야 한다.

$100 \times (1+?)^2 = 60$

$? = \left( \frac{60}{100} \right)^{1/2} - 1 \approx -0.225$

즉 연평균 23% 정도의 손실이 발생한 것으로 해석된다. 훨씬 더 합리적인 숫자라고 생각된다. 이런 방식으로 계산된 수익률을 CAGR (Compound Annual Growth Rate) 이라고 한다. 연평균 기하수익률 또는 연복리 수익률이라고도 불린다.

좀 더 일반적인 공식을 유도해보자. CAGR을 $r_p$ 라고 두고 (여기서 아랫첨자 $p$ 는 Portfolio를 의미)

연간 영업일수¹ $D$ ( $\approx$ 250)
최초 투자일 $t_0$ 의 투자대상 가격(또는 가치) $P_0$
최종 투자일 $t_1$ 의 투자대상 가격(또는 가치) $P_1$
총 투자 영업일수 $\Delta t = t_1 - t_0$

를 이용하면, $r_p$ 는 다음과 같이 구해진다.

$\frac{P_1}{P_0} = (1+r_p)^{\frac{\Delta t}{D}}$

$\therefore r_p = \left( \frac{P_1}{P_0} \right)^\frac{D}{\Delta t} - 1$

초과수익률

BM(Benchmark, 벤치마크) 수익률을 참고로 해야 할 때가 있다. 예를들어 작년 나의 투자수익률이 10% 였는데, 코스피 지수가 30% 올랐다고 생각해보자. 손실이 난 것은 아니지만, 그래도 기분이 썩 좋지는 않을 것이다. 이렇듯, 나의 투자수익률이 BM과 비교하여 상대적으로 어느 정도인지를 나타내는 지표가 초과수익률(Excess return)이다. Active return 이라고도 한다. 투자기간 동안의 BM의 CAGR을 $r_b$ 라고 하면, 초과수익률 $r_e$ 는 다음과 같이 계산된다.

$r_e = r_p - r_b$

변동성

변동성(Volatility)은 얼마나 안전하게(또는 위험하게) 투자하고 있는 지를 측정하는 지표이다. 변동성이 작을 수록 안전하다고 해석하면 된다. 일반적으로 변동성은 수익률의 표준편차²(Standard deviation) $\sigma$ 로 표현되는 경우가 많다.

투자전략의 수익률 변수 $R_p \in \mathbb{R}$
연률화 계수³ (Anualization factor) $\tau$

에 대해서, 변동성 $\mathbf{V}$ 는 다음과 같이 나타낼 수 있다. ⁴

$\sigma_p^2 = \mathbf{Var}[R_p] = \mathbf{E} \left[ (R_p-\mathbf{E}[R_p])^2 \right]$

$\mathbf{V} = \sqrt{\tau \mathbf{Var}[R_p]} = \sigma_p \sqrt{\tau}$

변동성의 해석

투자전략의 수익률이 정규분포를 따른다고 가정한다면, 변동성은 다음과 같이 해석할 수 있다. 예를들어 $\mathbf{V}$ = 4% 라면, 내 투자전략의 연수익률이 연 기대수익률⁵ $\tau \mathbf{E}[R_p]$ 을 중심으로 $\pm$ 4%의 범위에 있을 가능성이 약 2/3 ( $\approx$ 68.2%) 이라는 의미이다. 아래 확률밀도함수 참조.
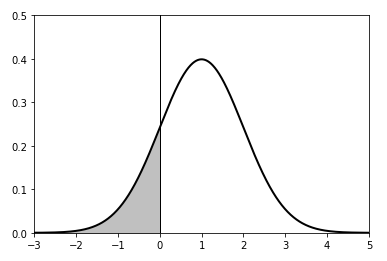
표준정규분포의 확률밀도함수 (출처: 위키피디아)
하지만 내 투자전략의 수익률이 정규분포를 따른다는 보장은 없다. 일반적으로 주식 등의 금융자산 수익률은, 정규분포가 아닌 Fat-tail 분포를 따른다고 알려져 있다. 따라서 해당 주식의 수익률이 특정 범주에 속할 가능성은 생각보다 낮을 수 있다. (금융자산들 간의 포트폴리오인) 특정 투자전략의 경우도 마찬가지라고 생각된다. 즉 위 사례를 다시 보면, $\pm$ 4%의 범위에 있을 가능성은 2/3 보다도 낮을 것이다.
표준정규분포와 Fat-tail 분포의 비교 (출처: PIMCO)

변동성은 목적에 따라 크게 두 가지 방식으로 측정할 수 있다.

사후적 변동성 (= 과거의 변동성)
사전적 변동성 (= 미래의 변동성)

사후적 변동성 (ex-post volatility)

ex-post는 라틴어로 사후(事後)라는 뜻이다. 즉 사후적 변동성이란, 투자성과가 발생한 후 그 결과를 확인하는 측면에서 측정하는 변동성을 의미한다. 실현 변동성(Realized volatility), 역사적 변동성(Historical volatility) 모두 같은 말이며, 그냥 변동성이라고 말하면 일반적으로 사후적 변동성을 의미한다.

사후적 변동성은 수익률의 샘플 표준편차(Sample standard deviation) 로 계산한다. 즉 투자전략의 과거 수익률 벡터 $\mathbf{r}_p = (r_{p1}, \cdots, r_{pm}) \in \mathbb{R}^m$ 에 대하여 샘플 표준편차 $s_p$ 를 구하면,

$\begin{aligned} \bar r_p &= \frac{1}{m} \sum_{j=1}^m r_{pj} \\ \sigma_p &= s_p = \left( \frac{1}{m} \sum_{j=1}^m (r_{pj} - {\bar r}_p)^2 \right)^{1/2} \end{aligned}$

이고, 사후적 변동성 $\mathbf{V}_h$ 은 다음과 같이 도출된다. (아랫첨자 $h$ 은 historical 을 의미한다)

$\mathbf{V}_h = s_p \sqrt{\tau}$

사전적 변동성 (ex-ante volatility)

ex-ante는 라틴어로 사전(事前)이라는 뜻이다. 즉 사전적 변동성이란, 투자성과가 발생하기 전에 미리 예측된 변동성을 의미한다. 어떻게 예측할 수 있을까? 핵심은 공분산 행렬(Covariance matrix)을 추정하는 데에 있다.

포트폴리오에서 현재 보유하고 있는 각 종목별 비중 벡터 $\mathbf{w}_p \in \mathbb{R}^d$ 및 종목별 수익률 확률변수 $\mathbf{X} \in \mathbb{R}^d$ 에 대해서, 포트폴리오 수익률의 분산(Variance)은 다음과 같이 계산된다.

$\mathbf{Var} [R_p] = \mathbf{Var} [\mathbf{w}_p^\mathsf{T} \mathbf{X}] = \mathbf{w}_p^\mathsf{T} \mathbf{\Sigma} \mathbf{w}_p$

여기서 $\mathbf{\Sigma} \in \mathbb{R}^{d \times d}$ 는 수익률의 공분산 행렬을 의미한다.

$\mathbf{\Sigma} = \mathbf{Var}[\mathbf{X}] = \mathbf{Cov}[\mathbf{X},\mathbf{X}] = \begin{bmatrix} \sigma_{11} & \cdots & \sigma_{1d} \\ \vdots & \ddots & \vdots \\ \sigma_{d1} & \cdots & \sigma_{dd} \end{bmatrix}$

따라서 사전적 변동성 $\mathbf{V}_f$ 은 다음과 같이 예측된다. (아랫첨자 $f$ 는 future 를 의미한다)

$\mathbf{V}_f = \sqrt{\tau \mathbf{Var}[R_p]} = \sqrt{\tau ~\mathbf{w}_p^\mathsf{T} \mathbf{\Sigma} \mathbf{w}_p}$

공분산 행렬의 추정

다시 한번 강조하자면, 사전적 변동성의 핵심은 공분산 행렬에 있다. 하지만 공분산 행렬을 엄밀히 추정하는 작업은 굉장히 어려운 분야에 해당하기 때문에, 이 블로그가 다룰 수 있는 영역을 벗어난다. 몬테카를로 시뮬레이션에 기반한 금융 시나리오 분석 등 학문적/현실적 요소가 가득하며, 글로벌 금융회사에서는 큰 돈을 들여 공분산 행렬 추정기법을 개발하고, 이를 자사의 리스크 관리에 활용한다. 따라서 이 블로그에서는 단순히 MLE (Maximum Likelihood Estimation)를 통해 공분산 행렬을 추정하거나, 또는 EWM (Exponentially weighted moving method) 방식으로 공분산 행렬을 계산하고 있다.

예를들어 MLE로 공분산 행렬을 추정해보자. 종목별 수익률 샘플 $\mathbf{x} = (\mathbf{x}_1, \cdots, \mathbf{x}_n)$ , $\mathbf{x}_i \in \mathbb{R}^d$ (즉 $d$ 개 종목의 수익률 벡터가 $n$ 개)이 주어졌다고 하면, 공분산 행렬 $\mathbf{\Sigma}$ 는 다음과 같이 추정된다.

$\begin{aligned} \mu &= \frac{1}{n} \sum^n_{i=1} \mathbf{x}_i \\ \mathbf{\Sigma} &= \frac{1}{n} \sum^n_{i=1} (\mathbf{x}_i - \mu) (\mathbf{x}_i - \mu)^\mathsf{T} \end{aligned}$

이와 같은 형태의 공분산 행렬을 샘플 공분산 행렬 (Sample covariance matrix) 이라고도 한다. 자세한 유도과정은 다변수 정규분포의 모수추정 을 참고.

Semi-deviation

변동성은 방향성을 고려하지 않는다. 예를들어 어떤 주식의 가격이, 상승할 때는 10% 씩 상승하고, 하락할 때는 고작 1% 정도만 하락한다고 가정해보자. 이 주식은 매우 훌륭한 주식일 가능성이 높다. 하지만 변동성을 계산할 때는 상승변동과 하락변동을 모두 고려하기 때문에, 어느 누군가는 이 주식의 투자위험이 다소 과대평가 되었다고 생각할 지도 모른다.

상승이나 하락, 즉 방향성을 고려하여 계산한 변동성을 Semi-deviation⁶이라고 한다.

Downside risk

Downside risk는 미리 정해놓은 목표수익률보다 낮은 수익률들에 대해서만 변동성을 계산한 것이다. 목표수익률 $\theta$ 와 연률화 계수 $\tau$ 에 대해, Downside risk $\mathbf{V}_{\le \theta}$ 는 다음과 같이 정해진다.

$\begin{aligned} \mathbf{Var}[R_p \le \theta] &= \mathbf{E} \left[ \min(0, R_p - \theta)^2 \right] \\ \mathbf{V}_{\le \theta} &= \left( \tau \mathbf{Var}[R_p \le \theta] \right)^{1/2} \end{aligned}$

Upside potential

Upside potential은 미리 정해놓은 목표수익률보다 높은 수익률들에 대해서만 변동성을 계산한 것이다. 마찬가지로 Upside potential $\mathbf{V}_{\gt \theta}$ 는 다음과 같이 정해진다.

$\begin{aligned} \mathbf{Var}[R_p \gt \theta] &= \mathbf{E} \left[ \max(0, R_p - \theta)^2 \right] \\ \mathbf{V}_{\gt \theta} &= \left( \tau \mathbf{Var}[R_p \gt \theta] \right)^{1/2} \end{aligned}$

Downside risk와 Upside potential의 정의에 의해, $\theta = \mathbf{E} [R_p]$ 인 경우에는 다음의 재미있는 성질이 발견된다.

$\begin{aligned} \mathbf{V}_{\le \mathbf{E} [R_p]}^2 + \mathbf{V}_{\gt \mathbf{E} [R_p]}^2 &= \tau \mathbf{E} \left[ \min(0, R_p - \theta)^2 \right] + \tau \mathbf{E} \left[ \max(0, R_p - \theta)^2 \right] \\ &= \tau \mathbf{E} \left[ \min(0, R_p - \theta)^2 + \max(0, R_p - \theta)^2 \right] \\ &= \tau \mathbf{E} \left[ (R_p - \mathbf{E} [R_p])^2 \right] \\ &= \mathbf{V}^2 \end{aligned}$

$\therefore \mathbf{V} = \sqrt{\mathbf{V}_{\le \mathbf{E} [R_p]}^2 + \mathbf{V}_{\gt \mathbf{E} [R_p]}^2}$

추적오차

BM 대비 상대적인 변동성을 계산한 값을 추적오차(Tracking error)라고 한다. 예를들어, 한국시장 전체에 투자하기 위해 코스피 인덱스 펀드에 가입했다고 가정해보자. 그런데 어떤 펀드는 코스피 인덱스와 매일 1% 이상씩 위아래로 차이가 나고, 또 다른 펀드는 매일 0.1% 정도만 차이가 난다고 하면, 과연 어느 펀드에 가입할까? 후자일 가능성이 높은 데, 이러한 경우를 추적오차가 작다고 얘기한다. ⁷ Active risk 라고도 부른다.

추적오차도 결국은 변동성이기 때문에, 측정하는 방법도 변동성과 거의 유사하다.

투자전략의 수익률 변수 $R_p \in \mathbb{R}$
BM 수익률 변수 $R_b \in \mathbb{R}$
연률화 계수 $\tau$

에 대해서, 추적오차 $\mathbf{TE}$ 는 BM 대비 초과수익률의 표준편차 $\sigma_e$ 로 계산된다.

$\sigma_e^2 = \mathbf{Var}[R_p-R_b]$

$\mathbf{TE} = \sqrt{\tau \mathbf{Var}[R_p-R_b]} = \sigma_e \sqrt{\tau}$

변동성과 마찬가지로, 추적오차 역시 목적에 따라 크게 두 가지 방식으로 측정할 수 있다.

사후적 추적오차 (= 과거의 추적오차)
사전적 추적오차 (= 미래의 추적오차)

사후적 추적오차 (ex-post tracking error)

투자성과가 발생한 후 그 결과를 확인하는 측면에서 측정하는 추적오차를 의미한다. 실현 추적오차(Realized tracking error), 역사적 추적오차(Historical tracking error) 모두 같은 말이며, 그냥 추적오차라고 말하면 일반적으로 사후적 추적오차를 의미한다.

사후적 추적오차는 BM 대비 초과수익률의 샘플 표준편차로 계산한다. 즉,

과거의 투자전략 수익률 벡터 $\mathbf{r}_p = (r_{p1}, \cdots, r_{pm}) \in \mathbb{R}^m$
과거의 BM 수익률 벡터 $\mathbf{r}_b = (r_{b1}, \cdots, r_{bm}) \in \mathbb{R}^{m}$
과거의 초과수익률 벡터 $\mathbf{r}_e \equiv \mathbf{r}_p - \mathbf{r}_b$ $= (r_{p1}-r_{b1}, \cdots, r_{pm}-r_{bm})$ $= (r_{e1}, \cdots, r_{em}) \in \mathbb{R}^m$

에 대하여 BM 대비 초과수익률의 샘플 표준편차 $s_e$ 를 구하면,

$\begin{aligned} \bar r_e &= \frac{1}{m} \sum_{j=1}^m r_{ej} \\ \sigma_e &= s_e = \left( \frac{1}{m} \sum_{j=1}^m (r_{ej} - {\bar r}_e)^2 \right)^{1/2} \end{aligned}$

이고, 사후적 추적오차 $\mathbf{TE}_h$ 는 다음과 같이 도출된다.

$\mathbf{TE}_h = s_e \sqrt{\tau}$

사전적 추적오차 (ex-ante tracking error)

투자성과가 발생하기 전에 미리 예측된 추적오차를 의미한다. 우선 포트폴리오의 각 종목별 초과비중 벡터를 $\mathbf{w}_e$ 를 다음과 같이 정의하자.

포트폴리오의 각 종목별 투자비중 벡터 $\mathbf{w}_p\in \mathbb{R}^d$
BM의 종목별 비중벡터 $\mathbf{w}_b\in \mathbb{R}^d$
초과비중 벡터 $\mathbf{w}_e \equiv \mathbf{w}_p - \mathbf{w}_b \in \mathbb{R}^d$

예를들어 포트폴리오의 종목수가 총 3개(BM 포함)이고, 각 종목별 투자비중이 주식:채권:원자재=40:30:30 및 BM의 종목별 비중이 주식:채권=50:50 인 경우라면, 각 비중벡터는 다음과 같이 쓸 수 있다.

$\mathbf{w}_p = \begin{bmatrix} 0.4 \\ 0.3 \\ 0.3 \end{bmatrix}, \mathbf{w}_b = \begin{bmatrix} 0.5 \\ 0.5 \\ 0.0 \end{bmatrix}, \mathbf{w}_e = \begin{bmatrix} -0.1 \\ -0.2 \\ 0.3 \end{bmatrix}$

이제 종목별 수익률 확률변수 $\mathbf{X} \in \mathbb{R}^d$ 에 대해서, 포트폴리오 초과수익률의 분산은 다음과 같이 계산된다.

$\mathbf{Var} [R_p-R_b] = \mathbf{Var} [\mathbf{w}_p^\mathsf{T} \mathbf{X} - \mathbf{w}_b^\mathsf{T} \mathbf{X}] = \mathbf{Var} [\mathbf{w}_e^\mathsf{T} \mathbf{X}] = \mathbf{w}_e^\mathsf{T} \mathbf{\Sigma} \mathbf{w}_e$

여기서 $\mathbf{\Sigma} \in \mathbb{R}^{d \times d}$ 는 수익률의 공분산 행렬을 의미한다. 따라서 사전적 추적오차 $\mathbf{TE}_f$ 은 다음과 같이 예측된다.

$\mathbf{TE}_f = \sqrt{\tau \mathbf{Var}[R_p - R_b]} = \sqrt{\tau ~\mathbf{w}_e^\mathsf{T} \mathbf{\Sigma} \mathbf{w}_e}$

위험조정수익률

변동성 대비 수익률을 위험조정수익률이라고 한다. 즉 내가 짊어진 위험부담에 비해 투자성과가 얼마나 좋았는지를 나타내는 상대지표라고 할 수 있다. 변동성과 수익률을 각기 어떤 값으로 설정하는가에 따라 여러가지 방식의 위험조정수익률을 측정한다.

Sharpe

투자전략의 변동성 대비 CAGR을 Sharpe 라고 한다. 즉 투자전략 자체의 변동성에 비해 투자전략 자체의 수익률⁸이 얼마나 좋았는지를 나타낸다. 가장 많이 사용되는 위험조정수익률 지표이다.

$\mathbf{Sharpe} = \frac{r_p}{\mathbf{V}}$

변동성 $\mathbf{V}$ 를 사후적 변동성 $\mathbf{V}_h$ 으로 할 것인가, 아니면 사전적 변동성 $\mathbf{V}_f$ 으로 할 것인가에 대해서는 뚜렷히 정해진 가이드라인이 없다. 각자의 상황에 따라 적절한 것을 골라서 사용하면 된다. 보통 Sharpe가 1 이상이면 양호한 투자전략으로 본다.

Sortino

투자전략의 Downside risk 대비 CAGR을 Sortino라고 한다. 투자전략이 감내하는 손실위험에 비해 투자수익률이 얼마나 좋았는지를 나타낸다. 이 블로그에서는 Downside risk의 목표수익률 $\theta = 0$ 을 선호한다.

$\mathbf{Sortino} = \frac{r_p}{\mathbf{V}_{\le 0}}$

정의에 의해 $\mathbf{V}$ 가 $\mathbf{V}_{\le 0}$ 보다 크므로, Sortino가 Sharpe보다 늘 큰 값임을 알 수 있다.

IR

투자전략의 추적오차 대비 초과수익률을 IR (Information Ratio)이라고 한다. 정보비율이라고도 부른다. 즉 투자전략의 BM대비 변동성에 비해 얼마나 초과수익률을 달성했는지를 나타낸다.

$\mathbf{IR} = \frac{r_e}{\mathbf{TE}}$

Sharpe와 마찬가지로, 추적오차 $\mathbf{TE}$ 를 사후적 추적오차 $\mathbf{TE}_h$ 으로 할 것인가, 아니면 사전적 추적오차 $\mathbf{TE}_f$ 으로 할 것인가에 대해서는 뚜렷히 정해진 가이드라인이 없다. 각자의 상황에 따라 적절한 것을 골라서 사용하면 된다. 보통 IR이 1 이상이면 양호한 투자전략으로 본다.

MDD

MDD (Maximum Drawdown)는 전체 투자기간 동안 경험한 최대손실폭을 말한다. 투자위험을 손실고통의 측면에서 측정한 값이며, 투자성과의 불확실성 측면에서, 변동성과 더불어 굉장히 중요한 의미를 지닌다. 실전에서는, 직전 고점 대비 손실률 중 최대값으로 계산된다.

(출처: meetinvest)

한 가지 주의할 점은, 초기 투자액을 기준으로 손실폭이 산출되는 것이 아니라, 직전 최대금액을 기준으로 한다는 사실이다. 예를들어 초기 투자액 100원이 200원으로 올랐다가 다시 100원으로 돌아갔다면, MDD는 0%가 아니라 -50% (200원 → 100원)이 된다.

우선 Drawdown 이 무엇인지를 알아야 한다. Drawdown은 (전체 투자기간이 아닌) 어느 특정 시점 기준에서 경험한 최대손실폭을 뜻한다. $t$ 시점에서의 주식가격(또는 투자전략의 가치)을 $P_t$ 라고 하면, $t$ 시점의 Drawdown $\mathbf{DD}_t$ 는 다음과 같이 정의된다.

$\mathbf{DD}_t = \frac{P_t}{\displaystyle \max_{0 \le k \le t} P_k} - 1$

$\mathbf{DD}_t$ 는 늘 음수가 된다. 따라서 MDD는 전체 투자기간 $T$ 중 (-) 방향으로 가장 큰 값(즉 최소값)으로 정의된다.

$\mathbf{MDD} = \min_{0 \le t \le T} \mathbf{DD}_t$

Beta

BM 수익률 대비 민감도(Sensitivity) 또는 탄력성(Elasticity)을 $\beta$ 라고 한다. 즉 BM 수익률이 1 만큼 변동했을 때 투자전략의 수익률이 얼마만큼 움직일 지를 측정하는 상대적인 지표가 된다. 주로 최소제곱법 (OLS: Ordinary Least Squares) 을 이용하여 $\beta$ 를 추정하게 된다.

우선 주요변수를 셋팅한다.

투자전략의 수익률 변수 $R_p \in \mathbb{R}$
BM 수익률 변수 $R_b \in \mathbb{R}$
투자전략의 수익률 중 BM 수익률로 설명이 안되는 오차항⁹ 변수 $\epsilon \in \mathbb{R}$

투자전략의 수익률을 BM 수익률 하나로 설명¹⁰할 수 있다고 가정하면, 상수 $\alpha, \beta \in \mathbb{R}$ 에 대해 $R_p$ 를 다음과 같이 선형회귀 방정식으로 표현할 수 있다.

$R_p = \alpha + \beta R_b + \epsilon$

수식전개의 편의를 위해, 각 수익률 변수의 기대값으로 중심축을 이동하면 $\alpha$ 가 제거된다. 즉

$Z_p \equiv R_p - \mathbf{E}[R_p]$
$Z_b \equiv R_b - \mathbf{E}[R_b]$

을 이용하면,

$\begin{aligned} R_p &= \alpha + \beta R_b + \epsilon \\ \mathbf{E}[R_p]&= \alpha + \beta \mathbf{E}[R_b] \\ R_p - \mathbf{E}[R_p] &= \alpha + \beta R_b + \epsilon - \mathbf{E}[R_p] \\ &= \beta (R_b - \mathbf{E}[R_b]) + \epsilon \end{aligned}$

$\therefore Z_p = \beta Z_b + \epsilon$

따라서 선형회귀 방정식은 $(\mathbf{E}[R_b], \mathbf{E}[R_p])$ 점을 지나가게 된다.

이제 $\beta$ 를 추정해보자. 최소제곱법은 오차항 $\epsilon$ 의 크기를 최소화 하는 방향으로 미지수를 추정하는 기법이다. $Z_p$ 의 샘플벡터를 $\mathbf{z}_p \in \mathbb{R}^m$ , $Z_b$ 의 샘플벡터를 $\mathbf{z}_b \in \mathbb{R}^m$ 라고 하고, 오차항 벡터 $\mathbf{e} \in \mathbb{R}^m$ 를 다음과 같이 정의하자.

$\mathbf{e} \equiv \mathbf{z}_p - \hat\beta \mathbf{z}_b$

여기서 $\hat\beta$ 는 $\beta$ 의 추정값을 의미한다. 미분을 이용하면 $\hat\beta$ 이 손쉽게 도출된다.

$\begin{aligned} \Vert \mathbf{e} \Vert^2 = \mathbf{e}^\mathsf{T} \mathbf{e} &= (\mathbf{z}_p - \hat\beta \mathbf{z}_b)^\mathsf{T} (\mathbf{z}_p - \hat\beta \mathbf{z}_b) \\ &= \mathbf{z}_p^\mathsf{T} \mathbf{z}_p - 2 \hat\beta \mathbf{z}_b^\mathsf{T} \mathbf{z}_p + \hat\beta^2 \mathbf{z}_b^\mathsf{T} \mathbf{z}_b \end{aligned}$

$\frac{\partial}{\partial \hat\beta} \Vert \mathbf{e} \Vert^2 = -2 \mathbf{z}_b^\mathsf{T} \mathbf{z}_p + 2 \hat\beta \mathbf{z}_b^\mathsf{T} \mathbf{z}_b = 0$

$\therefore \hat\beta = (\mathbf{z}_b^\mathsf{T} \mathbf{z}_b)^{-1} \mathbf{z}_b^\mathsf{T} \mathbf{z}_p$

통계지표로서의 $\beta$

위에서 최소제곱법으로 추정한 $\beta$ 값을 통계지표 측면에서 나타낼 수도 있다.

BM 과거수익률 벡터 $\mathbf{r}_b \in \mathbb{R}^m$ 와 샘플평균 ${\bar r}_b$

투자전략의 과거수익률 벡터 $\mathbf{r}_p \in \mathbb{R}^m$ 와 샘플평균 ${\bar r}_p$

에 대하여,

$\mathbf{z}_b = \mathbf{r}_b - {\bar r}_b \mathbf{1}_m$ ¹¹

$\mathbf{z}_p = \mathbf{r}_p - {\bar r}_p \mathbf{1}_m$

이므로,

$\begin{aligned} \hat\beta = (\mathbf{z}_b^\mathsf{T} \mathbf{z}_b)^{-1} \mathbf{z}_b ^\mathsf{T} \mathbf{z}_p &= \frac{\frac{1}{m} (\mathbf{r}_b - {\bar r}_b \mathbf{1}_m)^\mathsf{T} (\mathbf{r}_p - {\bar r}_p \mathbf{1}_m)}{\frac{1}{m} (\mathbf{r}_b - {\bar r}_b \mathbf{1}_m)^\mathsf{T} (\mathbf{r}_b - {\bar r}_b \mathbf{1}_m)} \\[13pt] &= \frac{\mathbf{Cov}[R_b, R_p]}{\mathbf{Var} [R_b]} \\[10pt] &= \rho \frac{s_p}{s_b} \end{aligned}$

여기서 $\rho \equiv \frac{\mathbf{Cov}[R_b, R_p]}{\sqrt{\mathbf{Var}[R_b] \mathbf{Var}[R_p]}}$ 는 투자전략의 수익률과 BM 수익률 간의 상관계수, $s_p$ 는 투자전략 수익률의 샘플 표준편차, $s_b$ 는 BM 수익률의 샘플 표준편차를 의미한다.

절편 $\alpha$ 의 억제

실험 관찰자의 사전지식 등으로 인해, 회귀방정식이 원점을 지날 것이라고 강한 확신을 하는 경우가 있다. 이럴 때에는 회귀방정식의 형태를 다음과 같이 가정할 수 있다. 즉, $\alpha=0$ 으로 놓는다.

$Y = \beta X + \epsilon$

애초에 $\alpha$ 가 없는 상태이므로, $\alpha$ 를 제거하기 위한 좌표변환 역시 필요없다. 마찬가지로 최소제곱법을 적용하여 $\beta$ 를 추정해보면, 변수 $X$ 의 샘플벡터 $\mathbb{x} \in \mathbf{R}^m$ 및 변수 $Y$ 의 샘플벡터 $\mathbf{y} \in \mathbb{R}^m$ 에 대하여,

$\hat\beta = (\mathbf{x}^\mathsf{T} \mathbf{x})^{-1} \mathbf{x}^\mathsf{T} \mathbf{y}$

Hit ratio

투자기간 중 수익이 발생한 구간의 비율을 단순 카운팅한 지표이다. 이 값이 크다면, 투자전략에서 손실이 발생하는 날보다 수익이 발생하는 날이 더 많다고 해석한다. 승률이라고도 한다. 투자전략 수익률 샘플들의 집합을 $\mathbf{R} = \{r_{i} \}$ 이라고 하면, (+) 수익률의 집합 $\mathbf{R}^+$ 과 (-) 수익률의 집합 $\mathbf{R}^-$ 을 정의할 수 있다.

$\begin{aligned} \mathbf{R}^+ &= \{ r_i \in \mathbf{R} \mid r_i > 0 \} \\ \mathbf{R}^- &= \{ r_i \in \mathbf{R} \mid r_i < 0 \} \end{aligned}$

$\mathbf{R}^+ \cup \mathbf{R}^- \cup \{ 0 \} = \mathbf{R}$

이제 Hit ratio $\mathbf{HR}$ 은 다음과 같이 정의된다.

$\mathbf{HR} = \frac{\mathbf{n}(\mathbf{R}^+)}{\mathbf{n}(\mathbf{R})}$

여기서 $\mathbf{n}(\cdot)$ 은 해당 집합의 원소의 갯수를 세어주는 연산자이다.

Profit-to-loss

평균적인 손실률 대비 수익률의 비율을 의미한다. 이 값이 크다면, 손실보다 수익이 상대적으로 더 화끈하게 발생한다고 해석한다. 평균손익비라고도 부른다. Hit ratio에서 언급한 집합 $\mathbf{R}^+$ , $\mathbf{R}^-$ 에 대해 다음과 같이 정의한다.

$\mathbf{PL} = \frac{\text{avg}(\mathbf{R}^+)}{\text{avg}(\mathbf{R}^-)}$

여기서 $\text{avg}(\cdot)$ 은 해당 집합 원소들의 평균값을 계산하는 연산자이다.

Consistency

투자성과의 지속성을 평가하기 위한 지표이다. 투자성과의 로그정규가격에 선형회귀분석을 시행한 후, R-Square를 취한다. 결과적으로는 투자성과의 누적수익률이 얼마나 선형(Linear)에 가까운 지를 측정하게 된다.

Consistency는 이 블로그에서의 필요에 의해 만들어진 개념이며, 학문적인 배경이 전혀 없는 지표이니 주의하기 바란다.

투자성과의 로그정규가격(Log normalized price) 변수를 $Q \in \mathbb{R}$ 라고 두자. 예를들어 과거의 투자성과에서 임의의 연속적인 시간벡터 $\mathbf{t} = [t_i] \in \mathbb{R}^m$ 에 대한 잔고액(또는 가격)을 추출하고 이를 벡터 $\mathbf{p} = [p_i] \in \mathbb{R}^m$ 라고 하면, $i$ 시점에서의 로그정규가격 샘플 $q_i$ 은 다음과 같이 정의된다.

$q_i = \ln \frac{p_i}{p_0}$

따라서 로그정규가격의 샘플벡터 $\mathbf{q} = [q_i] \in \mathbb{R}^m$ 은 다음과 같이 생성된다.

$\begin{matrix} \mathbf{t} = (t_0, t_1, t_2, \cdots, t_{m-1}) \\ \mathbf{p} = (p_0, p_1, p_2, \cdots, p_{m-1}) \\[5pt] \Downarrow \\[5pt] \begin{aligned} \mathbf{q} &= \textstyle (\ln \frac{p_0}{p_0}, \ln \frac{p_1}{p_0}, \ln \frac{p_2}{p_0}, \cdots, \ln \frac{p_{m-1}}{p_0}) \\ &= (q_0, q_1, q_2, \cdots, q_{m-1}) \end{aligned} \end{matrix}$

정의에 의해, 로그정규가격 샘플벡터의 첫번째 샘플 $q_0=0$ 이다. 즉 회귀방정식이 원점을 지날 것이라고 사전적으로 알고 있는 것이다. 따라서 로그정규가격 변수 $Q$ 와 시간변수 $T$ 간의 선형방정식을 다음의 형태로 가정할 수 있다.

$Q = \beta T + \epsilon$

최소제공법을 통해 추정한 $\hat\beta$ 을 이용하면, $Q$ 의 추정값 $\hat Q$ 을 알 수 있다. 따라서,

$\hat Q = \hat\beta T ~\Longrightarrow~ Q - \hat Q ~\overset{\text{let}}{=} ~ \hat\epsilon$

여기서 $\hat\epsilon$ 는 $\epsilon$ (= $Q - \beta T$ ) 와 전혀 다른 값임을 유의한다. 이제 로그정규가격 $Q$ 의 분산을 다음과 같이 분해할 수 있다.

$\begin{aligned} \mathbf{Var}[Q] &= \mathbf{Var}[\hat Q + \hat\epsilon] \\ &= \mathbf{Var}[\hat Q] + \mathbf{Var}[\hat\epsilon] + 2 \mathbf{Cov} [\hat Q, \hat\epsilon] \end{aligned}$

따라서 $\mathbf{R}^2$ (R-Square) 의 정의¹²에 의해, Consistency $\mathbf{C}$ 는 다음과 같이 나타낼 수 있다.

$\mathbf{C} = \mathbf{R}^2 \equiv 1 - \frac{\mathbf{Var}[\hat\epsilon]}{\mathbf{Var}[Q]}$

R-square의 실제 계산은 샘플분산을 통하는 경우가 많다. 각 샘플데이터에 대하여,

로그정규가격의 샘플평균 $\bar q = \mathbf{E}[Q] = \frac{1}{m} \sum_i q_i$
로그정규가격 추정값의 샘플평균 $\bar {\hat q} = \mathbf{E}[\hat Q] = \mathbf{E}[Q] = \bar q$
오차항 샘플 $\hat{\mathbf{e}} \equiv \mathbf{q} - \hat{\mathbf{q}} = [\hat e_i]$ 의 샘플평균 $\bar {\hat e} = \mathbf{E}[\hat\epsilon] = 0$

를 알 수 있으므로,

$m \mathbf{Var}[Q] = \sum_i (q_i - \bar q)^2 ~\overset{\text{let}}{=}~ \mathbf{TSS}$

$m \mathbf{Var}[\hat Q] = \sum_i (\hat q_i - \bar {\hat q})^2 = \sum_i (\hat q_i - \bar q)^2 ~\overset{\text{let}}{=}~ \mathbf{ESS}$

$m \mathbf{Var}[\hat \epsilon] = \sum_i \hat e_i^2 ~\overset{\text{let}}{=}~ \mathbf{RSS}$

여기서 각 용어의 의미는 다음과 같다.

TSS (Total Sum of Squares): 종속변수의 총 변동량
ESS (Explained Sum of Squares): 회귀식의 총 변동량
RSS (Residual Sum of Squares): 오차항의 총 변동량

따라서 Consistency 는 다음과 같이 계산된다. 이는 R-Square의 일반적인 표현식에 해당한다.

$\mathbf{C} = 1 - \frac{\mathbf{Var}[\hat\epsilon]}{\mathbf{Var}[Q]} = 1 - \frac{\mathbf{RSS}}{\mathbf{TSS}}$

참고로, R-Square를 직관적으로 이해하려면 아래 차트를 보는 게 좋다. 모든 샘플에 대하여 빨간색 사각형의 넓이를 합산한 것이 TSS이고, 파란색 사각형의 넓이를 한산하면 RSS가 나온다. 종속변수를 잘 추정하면 할 수록 RSS는 작아지고, R-Square는 1에 가까워진다.

(출처: 위키피디아)

R-Square와 상관계수의 관계

다음의 선형회귀 방정식을 살펴보자.

$\begin{aligned} Y &= \alpha + \beta X + \epsilon \\ \hat Y &= \hat\alpha + \hat\beta X \\ \hat \epsilon &\equiv Y - \hat Y \end{aligned}$

일반적인 선형회귀모형에서, $Y$ - $\hat Y$ 사이의 상관계수 제곱이 R-Square와 동일하다는 것은 잘 알려져 있는 성질이다.

$\mathbf{R}^2 = \rho^2 (Y, \hat Y)$

하지만 이 관계가 늘 맞는 것은 아니다. $\alpha=0$ 을 강제하지 않는 일반적인 선형회귀방정식이어야 한다는 전제조건이 반드시 필요하다. 이 경우 최소제곱법에 의해 $\hat\beta = \frac{\mathbf{Cov}[X,Y]}{\mathbf{Var}[X]}$ 이므로,

$\begin{aligned} \mathbf{Cov}[\hat Y, \hat \epsilon] &= \mathbf{Cov}[\hat\alpha + \hat\beta X, \hat \epsilon] \\ &= \hat\beta \mathbf{Cov}[X, \hat \epsilon] \\ &= \hat\beta \mathbf{Cov}[X, Y - \hat Y] \\ &= \hat\beta \mathbf{Cov}[X, Y - \hat\alpha - \hat\beta X] \\ &= \hat\beta \left( \mathbf{Cov}[X,Y] - \hat\beta \mathbf{Var}[X] \right) \\ &= 0 \end{aligned}$

따라서 종속변수 $Y$ 의 분산은 다음과 같이 좀더 간단하게 분해되고,

$\begin{aligned} \mathbf{Var}[Y] &= \mathbf{Var}[\hat Y + \hat \epsilon] \\ &= \mathbf{Var}[\hat Y] + \mathbf{Var}[\hat \epsilon] + 2 \mathbf{Cov}[\hat Y, \hat \epsilon] \\ &= \mathbf{Var}[\hat Y] + \mathbf{Var}[\hat \epsilon] \end{aligned}$

R-Square 는 더 산뜻한 형태로 표현된다.

$\mathbf{R}^2 = 1 - \frac{\mathbf{Var}[\hat\epsilon]}{\mathbf{Var}[Y]} = \frac{\mathbf{Var}[\hat Y]}{\mathbf{Var}[Y]} = \frac{\mathbf{ESS}}{\mathbf{TSS}}$

이제 $Y, \hat Y$ 간 상관계수의 정의에 의해 다음 전개를 얻는다.

$\begin{aligned} \rho^2 (Y, \hat Y) &= \frac{(\mathbf{Cov}[Y, \hat Y])^2}{\mathbf{Var}[Y] \mathbf{Var}[\hat Y]} \\[12pt] &= \frac{(\mathbf{Cov}[\hat Y + \hat \epsilon, \hat Y])^2}{\mathbf{Var}[Y] \mathbf{Var}[\hat Y]} \\[12pt] &= \frac{(\mathbf{Var}[\hat Y] + \mathbf{Cov}[\hat \epsilon, \hat Y])^2}{\mathbf{Var}[Y] \mathbf{Var}[\hat Y]} \\[12pt] &= \frac{\mathbf{Var}[\hat Y]}{\mathbf{Var}[Y]} \\[12pt] &= \mathbf{R}^2 \end{aligned}$

아쉽게도 Consistency는 이 관계를 만족하지 못한다. $\alpha=0$ 을 강제한 회귀방정식을 쓰기 때문이다. 이 경우 $\hat\beta \ne \frac{\mathbf{Cov}[Q,T]}{\mathbf{Var}[T]}$ 이므로, $\mathbf{Cov}[\hat Q, \hat \epsilon] = 0$ 을 보장할 수 없다. 따라서 위와 같은 전개가 불가능하다.

Rolling stats

투자전략의 성과가 측정되는 구간이 꽤 길다면, 전체 구간동안 측정한 투자성과는 다소 왜곡되었을 가능성이 있다. 이런 경우에 쓸 수 있는 대안은, 선호하는 구간(이를테면 1년)의 성과 데이터를 모두 추출하고, 이들의 분포를 확인해보는 것이다.

Rolling stats는 이 블로그에서의 필요에 의해 만들어진 개념이며, 학문적인 배경이 전혀 없는 지표이니 주의하기 바란다.

투자전략 전체 구간을 $0 \le t \le T$ 라고 하고, 전 구간에 대한 벡테스트 결과를 $\mathbf{B}$ 라고 하자. 상대적으로 짧은 하위 투자기간 $\ell \in \mathbb{R}$ ( $0 \lt \ell \lt T$ ) 에 대해서, 특정시점 $t$ 로부터 $\ell$ 기간 동안의 벡테스트 결과를 $B_\ell(t)$ 이라고 정의하고, 전체 구간에서 추출할 수 있는 모든 벡테스트 결과의 집합을 $\mathbf{B}_\ell$ 이라고 하자. 즉

$\mathbf{B} \xrightarrow{\text{sampling}} \mathbf{B}_\ell \equiv \{ B_\ell(0), \cdots, B_\ell(T-\ell)\}$

이제 어떤 성과지표 $\mathbf{F}$ 에 대하여, 벡테스트 $B_\ell(t)$ 의 성과지표를 $\mathbf{F}_\ell(t)$ 이라고 하고, 이들의 집합 $\mathbf{F}_\ell$ 을 다음과 같이 정의한다.

$\mathbf{F}_\ell \equiv \{ \mathbf{F}_\ell(0), \cdots, \mathbf{F}_\ell(T-\ell) \}$

예를들어 벡테스트 전구간이 500일 ( $T$ =500)이고, 더 짧은 구간인 250일 ( $\ell$ =250)에 대한 변동성 $\mathbf{V}$ 의 분포를 확인하고 싶다면,

$\begin{aligned} \mathbf{B}_{250} &= \{ B_{250}(0), B_{250}(1), \cdots, B_{250}(250) \} \\ \mathbf{V}_{250} &= \{ \mathbf{V}_{250}(0), \mathbf{V}_{250}(1), \cdots, \mathbf{V}_{250}(250) \} \end{aligned}$

Rolling stats의 중간값

하위 투자기간 성과지표 집합의 대표값을 정하고 싶을 때가 있다. 이 경우에는 하위 투자기간 $\ell$ 에 대한 성과지표 $\mathbf{F}_\ell$ 의 중간값(median)을 취한다. 상대적으로 단기적인 구간에 대해 기대되는 성과지표의 Proxy로 활용한다.

$\mathbf{F}_\ell^m \equiv \text{med}~\mathbf{F}_\ell$

예를들어 총 투자기간 중 250일(즉 1년) CAGR의 중간값은 다음과 같이 정해진다.

$\mathbf{CAGR}_{250}^m = \text{med} ~\mathbf{CAGR}_{250}$

손실 가능성

나의 투자전략에 $\ell$ 기간동안 투자했을 때의 손실 가능성 (Loss probability)을 측정한다. $\mathbf{CAGR}_\ell$ 의 확률밀도함수에서 0 이하의 넓이를 계산하면 된다.

현실적으로는 $\mathbf{CAGR}_\ell$ 의 확률밀도함수를 정밀하게 추정하는 것이 어렵기 때문에, (Hit ratio를 구하듯이) $\mathbf{CAGR}_\ell$ 중 (+) 수익률의 갯수를 센다.

$\begin{aligned} \mathbf{CAGR}_\ell^+ &\equiv \{ r_i \in \mathbf{CAGR}_\ell \mid r_i > 0 \} \\ \mathbf{CAGR}_\ell^- &\equiv \{ r_i \in \mathbf{CAGR}_\ell \mid r_i < 0 \} \end{aligned}$

$\mathbf{CAGR}_\ell^+ \cup \mathbf{CAGR}_\ell^- \cup \{ 0 \} = \mathbf{CAGR}_\ell$

이제 Loss probability $\mathbf{LP}$ 은 다음과 같이 정의된다.

$\mathbf{LP} \equiv \frac{\mathbf{n}(\mathbf{CAGR}_\ell^+)}{\mathbf{n}(\mathbf{CAGR}_\ell)}$

연간 영업일수는 국가별로 매해 다르다. 한국의 경우 보통 245-250일 정도이고, 미국은 대략 250-255일이다. 혼선을 없애기 위해, 특별한 언급이 없는 경우 이 블로그에서는 한국이든 미국이든 상관없이 250일로 고정하였다. 투자성과를 측정하는 데 있어서, 5-10일 정도의 차이가 그다지 Critical하지는 않다고 생각한다. ↩
수익률 표준편차를 이용하여 변동성을 측정하는 아이디어는 포트폴리오 이론의 대가인 해리 마코위츠가 처음 고안했다고 알려져 있다 ↩
연 단위의 변동성으로 변환하기 위한 계수이다. 예를들어 수익률 확률변수 $R$ 이 일간단위라면 $\tau$ = $D$ = 250 이고, 만약 주간단위라면 $\tau$ = 52 (총 52주 이므로) 이다. 여기서 $D$ 는 연간 영업일수를 의미한다. ↩
브라운 운동(Brownian motion) 또는 위너과정(Wiener process)에 따르면, 주가수익률의 분산은 시간에 비례한다. 따라서 주가수익률의 표준편차는 시간의 제곱근에 비례하게 된다. ↩
기대수익률 $\mathbf{E}(\cdot)$ 는 CAGR과는 다른 개념이다. 가장 단순한 방법으로, 산술평균 기대수익률(즉 수익률 샘플평균)을 쓰는 경우가 많다. 사후적 변동성을 계산할 때도 산술평균 기대수익률을 쓴다. 연률화 계수 $\tau$ 를 곱해줘야 하는 것도 잊지 말자. ↩
적절한 한글용어를 찾지는 못했다 ↩
개인투자자들에게 추적오차는 상대적인 중요도가 떨어지는 것으로 보인다. 개인투자자들은 BM 대비 상대적인 성과보다는, 절대수익 관점에서 성과를 평가하는 경우(물론 그렇지 않은 분들도 많다)가 많기 때문이다. 반면 기관투자자들에게 추적오차는 매우 중요한 개념이다. 기관투자자들의 운용성과를 판단하는 기준으로 추적오차가 흔히 활용되기 때문이다. 특히 상위기관으로부터 위탁 받아서 운용하는 자금에는, 추적오차 제약조건이 부과되는 경우가 많다. ↩
대부분의 금융관련 교과서나 투자서에서는 Sharpe를 조금 다르게 측정한다. 즉 투자전략 자체의 수익률을 그대로 쓰는 게 아니라, 안전자산(무위험자산 또는 Risk-free)의 수익률 대비 초과수익률로 쓰는 경우가 많다. 개념적으로는 그게 좀더 맞는 표현인 것 같긴 하다. 적어도 예금이자보다는 더 벌어야지 수익이 났다고 주장할 수 있지 않은가. 하지만 이 블로그에서는 안전자산의 수익률은 고려하지 않았다. 안전자산의 정의가 매우 애매하고, 측정하는 사람마다 천차만별이기 때문에, 성과측정에 혼선을 준다고 판단하였다. ↩
Residual factor, Idiosyncratic error, Specific error, Specific factor, White noise 등으로 불린다. ↩
Sharpe의 Single-factor model 이라고 한다. 이를 확장하면 Multi-factor model이 된다. ↩
모든 원소가 1인 벡터를 의미한다. 즉 $\mathbf{1}_m \equiv (1, \cdots, 1) \in \mathbb{R}^m$ ↩
종속변수의 분산 중 회귀모형으로 설명이 불가능한 부분을 제외한 비율. 결정계수 (Coefficient of determination) 또는 설명력이라고도 한다. ↩

Written on February 20th, 2018 by quanty

Feel free to share!