Elastic Asset Allocation

# Asset allocation

Keller 교수의 Elastic Asset Allocation 논문을 리뷰하였다. Dual momentum의 수익률을 이기는 전략을 찾는 것이 원래의 목표였으나, Elastic Asset Allocation의 Original version 만으로는 목표달성이 힘들었다. 따라서 논문의 전략을 일부 수정하였고, 그 과정을 기록하였다.

Motivation
논문개요
포트폴리오 결정 프로세스
논문의 백테스트
실전 백테스트
- 매매규칙
- 결과
전략 비틀기
- 아이디어
- 결과
Conclusions

Motivation

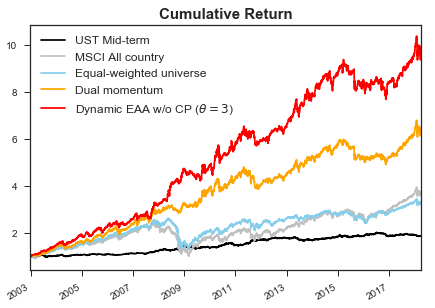
다음 차트는 2003년 이후 7개의 자산군(미국주식, 선진국주식, 신흥국주식, 원자재, 미국 부동산, 미국 High-yield, 미국 중기채)에서 Dual momentum 전략(노랑) 으로 투자했을 때의 투자성과를 보여준다. (백테스트 방법론에 대한 자세한 설명은 아래에서 다룬다)

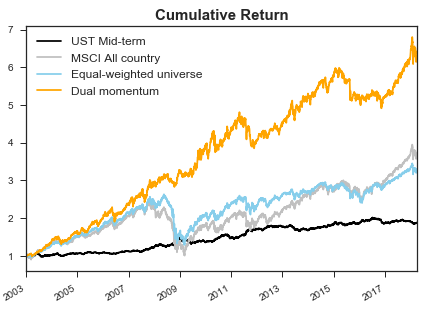
여기서 두 가지의 의문점을 가지게 되었다.

Dual momentum 보다 우월한 모멘텀 전략을 만들 수 있을까?
2015년의 Drawdown 구간을 견딜 수 있는 아이디어가 없을까?

특히 2번은 꽤 오랜기간 동안의 고민이었다. (어느 특정 자산군이 아닌) 다양한 자산군에서 모멘텀 전략을 취하는 경우, 그게 어떠한 형태의 모멘텀 전략이라 하더라도, 2015년 이후의 1-2년간 Drawdown이 발생하는 것을 피하기가 힘들었다. ¹ 모멘텀 스코어가 높은 자산을 선택하면, 보유기간 동안 반락하여 손해를 보는 경우가 다반사였고, 그러한 현상이 오랫동안 지속되었다.

그래서 생각한 것은, 동적인 포트폴리오 비중조절과 현금관리를 통해 이를 해결할 수 있지 않을까였다. 이 논문은 그러던 와중에 찾게 된 것이다.

논문개요

이 포스트는 투자논문 A Century of Generalized Momentum: From Flexible Asset Allocation (FAA) to Elastic Asset Allocation (EAA) 에 대한 리뷰와 추가적인 실험결과를 기록하였다. 이 논문은 Wouter J. Keller (네덜란드 암스테르담 대학교수)와 Adam Butler (ReSolve 자산운용 대표)가 공동 집필하였으며 2014년에 발표하였다.

논문의 내용은 전형적인 모멘텀 전략의 연장선에 있다. 즉 (사전에 정의된) 모멘텀 지표가 큰 자산에 투자하자는 것이 결론이다. 유용한 모멘텀 지표의 개발은 오랫동안 수많은 논문들의 연구주제가 되어왔다. 예를들어, Antonacci의 듀얼모멘텀 전략은 가격 모멘텀을 Time-series와 Cross-sectional로 구분하여 투자의 수익성과 안정성을 동시에 강화했다. 이 논문에서는 독자적인 모멘텀 지표의 소개와 더불어 포트폴리오 비중결정의 논리를 동시에 제공하였다. 저자는 이를 Generalized momentum 이라고 이름을 붙였는데, 기존의 다른 모멘텀 지표들 보다 유연한 Framework을 제공한다는 측면에서 제법 적절한 명칭이라고 생각된다.

포트폴리오 결정 프로세스

논문에서는 다음의 프로세스를 통해 포트폴리오 비중을 결정한다.

Generalized momentum: 좀더 일반화된 모멘텀 지표를 정의하고, 자산별로 스코어링
Asset selection: 모멘텀 지표가 큰 자산들을 선택
Crash protection: 현금관리(Cash management) 전략
Final portfolio: 포트폴리오 비중 최종결정

이를 Elastic Asset Allocation (이하 EAA) 이라고 한다.

Generalized momentum

우선 각 자산 $i$ 에 대해서 다음의 세 가지를 정의한다.

자산 $i$ 의 가격모멘텀 $\mathbf{R}_i$ : 가격 모멘텀을 정의하는 방식은 여러가지가 있다. 가장 흔한 방식으로는, 해당 자산가격의 12개월² 수익률을 쓴다. 논문에서는 1, 3, 6, 12개월에 대하여, T-bill 대비 초과수익률의 평균값을 썼다³. 가격 모멘텀이 큰 자산을 선호한다.

자산 $i$ 와 동일가중 유니버스 지수와의 상관계수 $\mathbf{C}_i$ : 투자 유니버스 구성종목들을 동일가중하여 생성된 포트폴리오와의 12개월 상관계수를 측정하였다. 상관계수가 낮은 자산을 선호한다.
자산 $i$ 의 변동성 $\mathbf{V}_i$ : 12개월 수익률의 표준편차로 측정한다. 변동성이 낮은 자산을 선호한다.

이제 자산 $i$ 의 모멘텀 스코어 $z_i$ 를 다음과 같이 정의하자. 논문에서는 이를 Generalized momentum score 라고 부른다.

$z_i \equiv \begin{cases} \mathbf{R}_i^\alpha (1-\mathbf{C}_i)^\beta \mathbf{V}_i^{-\gamma} & \text{if} ~~\mathbf{R}_i \gt 0 \\[8pt] 0 & \text{otherwise} \end{cases}$

여기서 $\alpha, \beta, \gamma \in \mathbb{R}_{\ge 0}$ 는 각각 $\mathbf{R}_i$ , $\mathbf{C}_i$ , $\mathbf{V}_i$ 에 대한 Elasticity⁴ (투자전략의 이름인 Elastic Asset Allocation 은 여기서 따온 것으로 추측) 라고 하며, 나중에 최적화의 대상이 된다. $\mathbf{R}_i$ , $1-\mathbf{C}_i$ , $\mathbf{V}_i$ 모두 양의 실수이므로,

가격모멘텀 $\mathbf{R}_i$ 가 클 수록
상관계수 $\mathbf{C}_i$ 가 작을 수록
변동성 $\mathbf{V}_i$ 가 작을 수록

모멘텀 스코어 $z_i$ 가 커진다는 사실을 알 수 있다.

상관계수 $\mathbf{C}_i$ 와 변동성 $\mathbf{V}_i$ 를 왜 반영했을까

저자는 포트폴리오의 변동성을 낮추고자 하였다. $n$ 개 종목으로 구성되어 있는 포트폴리오의 변동성 $\mathbf{V}_p$ 는, 비중벡터 $\mathbf{w}=[w_i] \in \mathbb{R}^n$ 및 공분산행렬 $\mathbf{\Sigma} = [\sigma_{ij}] \in \mathbf{R}^{n \times n}$ 에 대하여 다음과 같이 나타낼 수 있다.

$\begin{aligned} \mathbf{V}_p^2 &= \mathbf{w}^\mathsf{T} \mathbf{\Sigma} \mathbf{w} \\ &= \sum_i w_i^2 \sigma_{ii} + 2 \sum_{j \ne k} w_j w_k \sigma_{jk} \\ &= \sum_i w_i^2 \sigma_{i}^2 + 2 \sum_{j \ne k} w_j w_k \sigma_{j} \sigma_{k} \rho_{jk} \end{aligned}$

따라서 다른 조건이 모두 동일하다고 할 때, 변동성 $\mathbf{V}_i$ (= $\sigma_i$ ) 가 높은 자산 $i$ 의 비중 $w_i$ 를 줄이면 포트폴리오 변동성 $\mathbf{V}_p$ 이 작아질 것은 자명하다. 상관계수의 경우에는 약간 애매하다. 상관계수는 자산과 자산간의 일대일 관계이므로, 특정자산 $i$ 에 대해서 $n-1$ 개의 상관계수가 생성되고, 이들을 모두 고려하려면 모멘텀 스코어의 차원이 매우 커지게(즉 독립변수가 많아지게) 된다. 이 논문에서는 문제를 단순화하기 위해, 동일가중(즉 $w_i=1/n$ ) 유니버스 지수와의 상관계수 $\mathbf{C}_i$ 하나로 통일한 것으로 보인다.

Asset selection

$n$ 개의 자산 중, 위에서 정의한 모멘텀 스코어를 기준으로 상위 $m$ 개의 자산을 선택한다. 논문에서는

$m = \min \left( 1+\sqrt{n}, ~n/2 \right)$

라는 공식을 쓰는데, 논문에 그 이유는 나와있지 않았다. 아무래도 백테스트 과정에서 적절한 논리를 찾은 듯하다. 하지만 꼭 이렇게 할 필요는 없어 보이며, 전체 유니버스 종목 갯수 $n$ 의 30% 수준에서 선택하면 무리가 없을 것으로 생각된다.

Crash protection

Crash protection은 현금관리 전략이다. 즉 전체 예산 중 얼마만큼을 현금에 할당할 지를 결정한다. Crash protection 비율 $w_{cp}$ 은 전체 가격모멘텀 집합 $\{ \mathbf{R}_i \}$ 의 원소 중, (+)가 아닌 값의 비율을 의미한다.

$w_{cp} \equiv \frac{\mathbf{n}(\{ i \mid \mathbf{R}_i \le 0 \})}{n}$

여기서 $\mathbf{n}(\cdot)$ 는 집합의 원소 갯수를 세어주는 연산자이다. 참고로 논문에서는, 현금의 proxy로 미국채 10년물(UST 10Y)을 쓰고 있다.

Final portfolio

모멘텀 스코어 $z_i$ 가 내림차순으로 정열되어 있다고 가정해도 일반성을 잃지 않는다⁵. 이 경우 자산은 1 부터 $m$ 까지 선택되어 있을 것이다. 따라서 최종 포트폴리오는 다음과 같이 정해진다.

$w_i = \frac{z_i}{\sum_{j=1}^m z_j} (1 - w_{cp})$

Special cases

저자는 논문에 나오는 모멘텀 스코어를 Generalized momentum 이라고 불렀는데, 이유가 있다. 기존의 다른 모멘텀 스코어를 포함하는 개념으로 이해할 수 있기 때문이다. 예를 들면, (여기에서는 $w_{cp}=0$ 라고 하자)

Dual momentum ( $\alpha=\beta=\gamma=0$ )

$w_i = \frac{1}{m}$

동일가중 ( $\mathbf{R}_i \gt 0$ 조건 제거, $\alpha=\beta=\gamma=0$ )

$w_i = \frac{1}{n}$

Naive Risk-parity ( $\gamma=1$ , $\alpha=\beta=0$ )

$w_i = \frac{1}{\mathbf{V}_i} \frac{1}{\sum_{j=1}^m (1/\mathbf{V}_j)}$

논문의 백테스트

논문의 백테스트는 다음의 순서로 진행되었다.

IS 테스트 (In-sample test): Elasticity 변수를 최적화하여 두 개의 주요 모델 도출
OS 테스트 (Out-of-sample test): 도출된 모델의 검증

한 가지 특이할 만한 점은, 논문이 제시하는 전략이 다양한 자산군들에서도 유효한지를 검증하기 위해, 총 세가지의 유니버스에 대해 백테스트를 진행하였다는 점이다.

Global multi-asset small univ ( $n$ =7): S&P500, EAFE, EEM, US Tech, Japan Topix, UST 10Y, US HY
US-sector univ ( $n$ =15): 10개의 US Equity sector + 5개의 US Bond sector (UST 10Y, UST 30Y, Muni, IG, HY)
Global multi-asset large univ ( $n$ =38): Global multi-asset small univ + US-sector univ + 기타 (논문참조)

한편 IS 테스트를 통해, 각 자산별 모멘텀 스코어 $z_i$ 에서 변동성 $\mathbf{V}_i$ 의 영향이 생각보다 크지 않다는 사실을 발견했다는 내용이 논문에 나온다. 따라서 저자는, IS를 포함한 모든 백테스트에서 모멘텀 스코어를 다음의 형태로 변경하여 사용하였다. 최적화의 대상은 이제 $\alpha, \beta$ 가 되었다.

$z_i = \begin{cases} \mathbf{R}_i^\alpha (1-\mathbf{C}_i)^\beta & \text{if} ~~\mathbf{R}_i \gt 0 \\[8pt] 0 & \text{otherwise} \end{cases}$

논문의 표현에 따르면, $\alpha$ 는 특정자산에 비중이 얼마나 쏠리는지(Concentration)를 조절하고, $\beta$ 는 포트폴리오 헷징을 통해 투자성과의 안정성을 조절한다.

Calmar ratio

IS 테스트 및 OS 테스트에 들어가기 앞서, 우선 이 논문에서 주요 성과지표로 활용하고 있는 Calmar ratio에 대해 소개한다. Calmar ratio $\mathbf{CR}_t$ 는 위험조정수익률의 한 종류로서, 초과수익률과 MDD간의 비율을 의미한다.

$\mathbf{CR}_t \equiv \frac{\mathbf{CAGR}-t}{\mathbf{MDD}}$

여기서 $t$ 는 목표수익률을 뜻한다. 이를테면 $\mathbf{CR}_5$ 는 목표수익률 5%를 초과하는 위험조정수익률이다. Calmar ratio는 Sharpe의 MDD 버전이라고 이해하면 쉽다. 논문의 저자는, 장기투자하는 경우에는 Tail-risk가 매우 중요해지기 때문에, Sharpe보다는 Calmar ratio가 더 의미있는 지표라고 주장하였다.

IS 테스트

Elasticity 변수인 $\alpha$ , $\beta \in \mathbb{R}_{\ge 0}$ 를 최적화하는 과정이다. $\alpha$ 와 $\beta$ 를 일정간격(Grid)으로 나누어서 여러 ( $\alpha, \beta$ ) 조합을 만든다. 하나의 ( $\alpha, \beta$ ) 조합은 결국 하나의 EAA 전략에 해당한다. 각 ( $\alpha, \beta$ ) 조합에 대하여 다음의 백테스트를 수행하였다.

기간: 1914년 4월 - 1964년 3월 (50년간)
해당 ( $\alpha, \beta$ ) 조합으로 매월말 포트폴리오 구성 (월간 리밸런싱)
50년간의 CAGR과 MDD를 Calmar Scatter⁶에 표시

모든 ( $\alpha, \beta$ ) 조합에 대하여, 다음의 Calmar scatter를 얻게 된다.

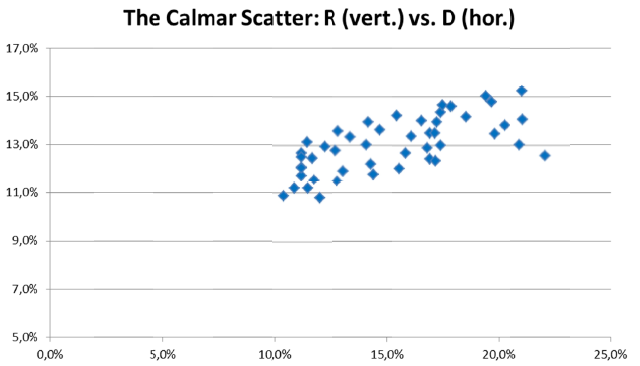
저자는 방어적인 투자의 목표수익률을 5%, 공격적인 투자자의 목표수익률을 10%로 보았다. 따라서 (Risk-Return profile에서 Efficient frontier를 그리는 것과 마찬가지로) Calmar ratio $\mathbf{CR}_5$ , $\mathbf{CR}_{10}$ 를 극대화하는 접선(Calmar frontier)를 그렸다. 그리고 해당 접점의 ( $\alpha, \beta$ ) 조합을 각각 Golden defensive model, Golden offensive model이라고 정의하였다.

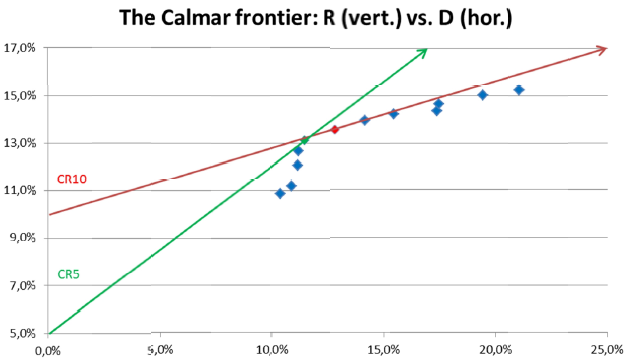
결과적으로 다음의 두 가지 모델을 도출하게 된다.

Golden Defensive model ( $\alpha = \beta = 0.5$ )

$z_i^{d} = \sqrt{\mathbf{R}_i (1-\mathbf{C}_i)} ~~~(\text{if} ~~\mathbf{R}_i \gt 0)$

Golden Offensive model ( $\alpha=2$ , $\beta=1$ )

$z_i^{o} = \mathbf{R}_i^2 (1-\mathbf{C}_i) ~~~(\text{if} ~~\mathbf{R}_i \gt 0)$

OS 테스트

IS 테스트에서 도출한 두 개의 모델 각각의 Out-of-sample 성과가 어땠는지를 확인해본다. 테스트 구간은 1964년 4월부터 2014년 8월까지 총 50년간(IS 기간과 동일)이다.

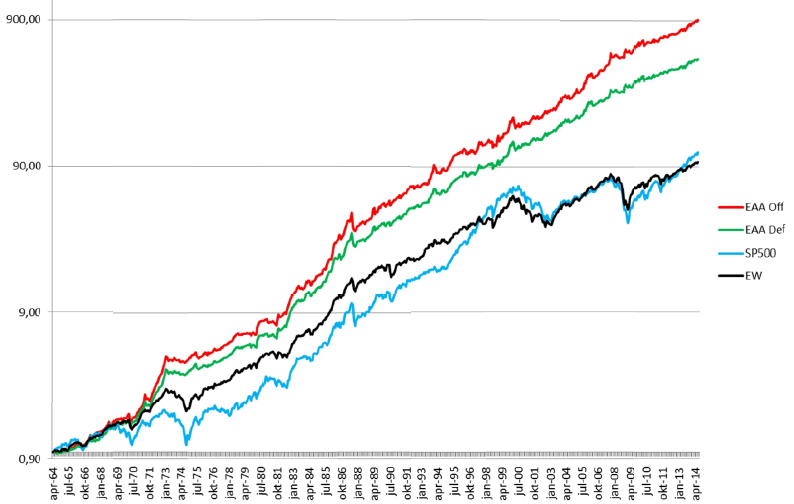
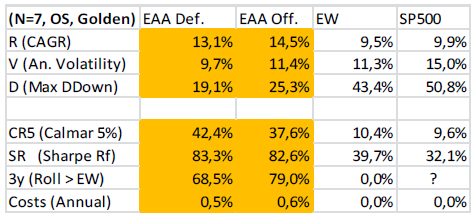
Cumulative return cum_dm

Statistics cum_dm

연수익률 13-15% 수준으로 동일가중 및 미국주식시장 대비 양호한 성과를 기록하였다.
변동성이 동일가중 포트폴리오에 비해 크게 개선되었다고 보기는 힘들었으나,
MDD는 동일가중, 미국주식시장의 50% 이하로 축소되었다.
결과적으로, 위험조정수익률(Calmar 및 Sharpe) 측면에서 양호한 성과를 보였다.

실전 백테스트

논문에서 제시한 두 개의 Golden 전략, 즉 Defensive model과 Offensive model을 실제로 백테스트해보자. 비교를 위해, Dual momentum 과 동일가중(EW: Equal-weighted) 전략도 포함하였다.

유니버스( $n$ =7): SPY(미국주식), EFA(선진국주식), EEM(신흥국주식), DBC(원자재), VNQ(미국 부동산), HYG(미국 High-yield), IEF(미국 중기채)
백테스트 기간: 2002.12.31 ~ 2018.03.31 (약 15년)
Monthly rebalancing
매매비용 10bp
Gross exposure 99% (매매비용 인출을 감안)
Cash asset: IEF(미국 중기채)

매매규칙

투자의사결정: 매월 마지막 영업일
- EAA: 모멘텀 스코어 $z_i$ 에 따라 자산을 선택하고 비중결정한다.
- Dual momentum: 가격모멘텀 $\mathbf{R}_i$ 에 따라 자산을 선택하고, 동일가중한다.
- EW: 유니버스 내 전종목을 동일가중한다.
매매: 매월 첫번째 영업일
- 전일 투자의사결정된 포트폴리오가 전월의 포트폴리오와 다른 경우에 한해, 당일 종가(Adjusted)로 매매한다.
- 만약 어떤 종목이 시장에서 아직 거래되지 않는다면, 해당 종목의 기초지수를 이용하여 그 종목의 시장가격을 역으로 추정한다.

결과

Dual momentum 전략과의 직접적인 비교를 위해, 일단은 Crash protection을 적용하지 않았다. 백테스트 결과는 다음과 같다. 결론부터 말하자면, CAGR 측면에서 EAA의 Golden 전략으로 Dual momentum을 이길 수는 없었다. 각 성과지표에 대한 자세한 설명은 투자성과의 측정을 참고.

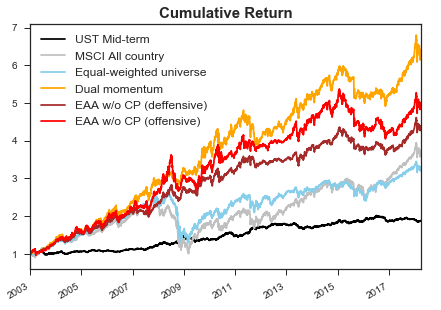
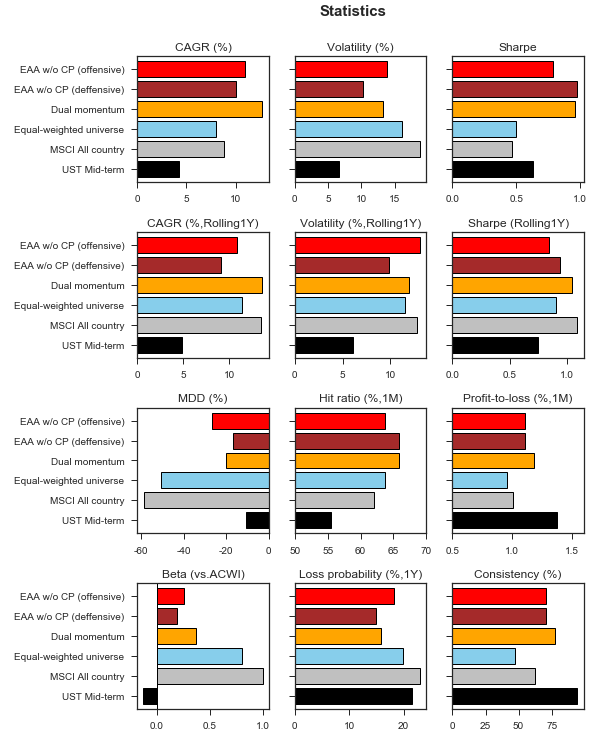
EAA w/o CP (Crash protection을 적용하지 않은 EAA 전략, Offensive는 빨강색, Defensive는 갈색)은 연평균 10-11%의 수익률을 보인 반면, Dual momentum(노랑)의 연평균수익률은 12-13% 수준이었다.
Defensive model의 변동성과 MDD는 Dual momentum 보다 낮았고, 이에따라 Sharpe는 Dual momentum과 비슷한 수준을 유지했다. 하지만 1-year rolling으로 관측하면, Dual momentum의 Sharpe가 가장 높았다.
Offensive model의 모든 성과측면에서 Dual momentum 보다 열등했다.

Offensive model ( $\alpha=2$ )의 변동성이 높은 이유는 무엇일까? 다음은 각 리밸런싱 시점에서의 포트폴리오에서 편입비중이 가장 큰 자산의 비중을 시계열로 나타낸 것이다.

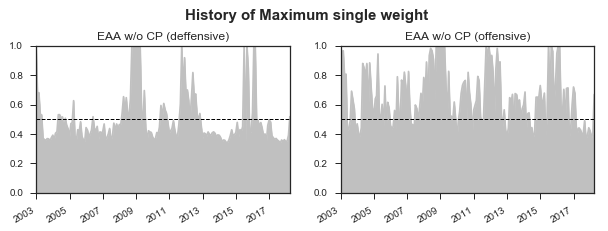
여기서 EAA의 독특한 성질을 알 수 있다. 포트폴리오 비중을 Elasticity 로 조절하기 때문에, $\alpha$ 가 커지면 커질 수록 편입비중은 더 빠른 속도로 커지고, 결과적으로 특정자산에의 쏠림현상이 커지는 경향이 있다.

논문에서 채택한 두 개의 모델보다 더 좋은 것을 찾을 수 있지 않을까? 다음은 0 이상의 $\alpha, \beta$ 를 0.2 단위의 Grid로 나누고, 모든 경우의 수에 대해 백테스트를 수행해 본 결과이다.

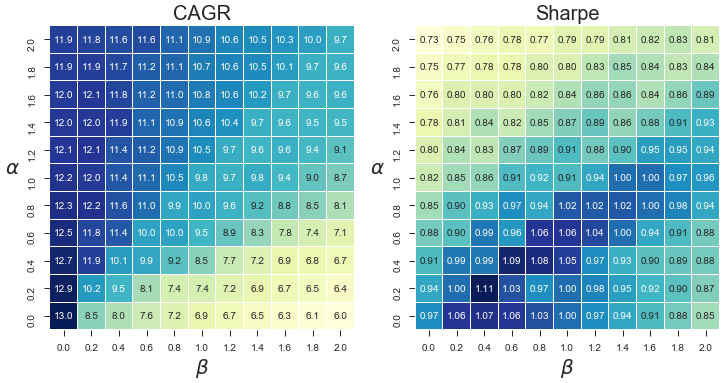
그 어떤 ( $\alpha, \beta$ ) 조합을 사용하더라도, Dual momentum의 CAGR을 뛰어넘을 수 없었다. 재미있는 것은, 모멘텀 스코어 $z_i$ 에 $\beta$ 가 조금이라도 반영되는 순간, CAGR의 레벨이 크게 하락한다는 사실이다. 생각해보면 너무나 당연하다. Dual momentum과 EAA는 전혀 다른 게임을 하고 있기 때문이다. Dual momentum은 가격모멘텀 $\mathbf{R}_i$ 을 최우선 가치로 삼고 해당값을 극대화하기 위해 노력한다. 반면 EAA는 상관계수 $\mathbf{C}_i$ 를 줄이기 위한 시도도 병행한다. 실험을 진행하면 진행할 수록, 가격모멘텀 $\mathbf{R}_i$ 만으로 자산을 선정하는 프로세스(즉 Dual momentum)는, 그 자체만으로도 굉장히 탁월한 전략(CAGR 측면에서)인 것으로 생각된다.

Dual momentum의 수익률을 이기는 건 애초에 불가능한 미션이었던 것일까?

전략 비틀기

아이디어

논문의 논리에 너무 매몰되지 말고, 전략을 조금 수정해보자. 바로 위의 Heat-map을 살펴보면, 상관계수 $\mathbf{C}_i$ 를 고려하여 자산을 선택하는 것은, 전략의 수익률을 다소 희생해야 하는 것을 내포하고 있는 것으로 추측된다. 따라서

아이디어 1. 모멘텀 스코어(Generalized momentum) $z_i$ 을 기준으로 자산을 선택하는 것이 아니라, (Dual momentum의 방식대로) 가격모멘텀 $\mathbf{R}_i$ 을 기준으로 선택한다.

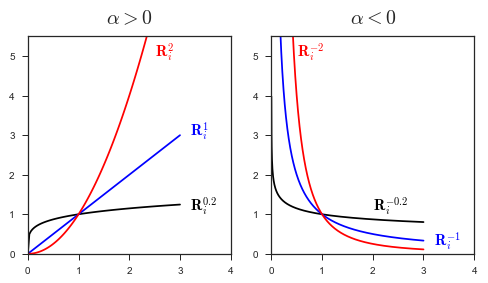
한편 ( $\alpha, \beta$ )의 조합을 미리 정해놓는 것이 아니라, 리밸런싱 할 때마다 동적으로 의사결정하게 하면 어떨까? 문제를 단순화 시키기 위해, $\beta=1$ 로 고정하면, 다음의 모멘텀 스코어를 얻게 된다.

$z_i \equiv \begin{cases} \mathbf{R}_i^\alpha (1-\mathbf{C}_i) & \text{if} ~~\mathbf{R}_i \gt 0 \\[8pt] 0 & \text{otherwise} \end{cases}$

각 자산의 수익률 확률변수 $\mathbf{X} = (X_1, \cdots, X_n)$ 에 대하여, 자산별 모멘텀 스코어 $z_i$ 를 해당 자산의 기대수익률 $\mathbf{E}[X_i]$ 로 가중한 값을 총 모멘텀 $\mathbf{M}$ 이라고 정의하자. $\mathbf{M}$ 은 $\alpha$ 의 함수가 된다.

$\mathbf{M} \equiv \mathbf{E}[X_1] z_1 + \cdots + \mathbf{E}[X_n] z_n = \mathbf{E}[\mathbf{X}]^\mathsf{T} \mathbf{z} = \mathbf{M}(\alpha)$

여기서 $\mathbf{z} = (z_1, \cdots, z_n)$ , $\mathbf{E}[\mathbf{X}] = (\mathbf{E}[X_1], \cdots, \mathbf{E}[X_n])$ 이다. 이 총 모멘텀 $\mathbf{M}$ 을 최대로 만드는 $\alpha$ 값을 찾는다. 단 EAA 전략의 특성상, $\alpha$ 가 너무 크거나 작으면 특정 자산에 비중이 과도하게 쏠리는 현상이 생길 수 있다. 따라서 어떤 실수 $\theta \gt 0$ 에 대해, $\alpha$ 를 $\pm \theta$ 내의 값으로 제한하자.

아이디어 2. 매 리밸런싱 시점별로, 다음과 같이 총 모멘텀 $\mathbf{M}$ 를 최대화하는 Elasticity $\alpha^*$ 를 찾고(Grid search), 이를 통해 포트폴리오 비중을 결정한다.

$\alpha^* = \underset{|\alpha| \le \theta}{\arg \max} ~\mathbf{E}[\mathbf{X}]^\mathsf{T} \mathbf{z}$

참고로 논문에서는 $\alpha \in \mathbb{R}_{\ge 0}$ 의 제약조건이 있으나, 여기에서는 이를 제거하였다. 이를 통해, 가격모멘텀 $\mathbf{R}_i$ 값이 크더라도 Mean-reverting 하여 반락할 가능성에 대해서, 해당 자산의 비중을 상대적으로 낮출 논리를 갖추었다.

결과

다음은 위의 아이디어를 백테스트에 적용한 누적수익률 차트이다. $\theta=3$ (즉 $\alpha$ 의 선택범위를 $\pm 3$ 으로 제한)으로 설정하였다. CAGR 및 Sharpe 측면에서 Dual momentum 대비 양호한 성과를 확인할 수 있다. (Sharpe는 맨 아래의 Stats 차트로 확인)

매 리밸런싱 시점에서 결정된 $\alpha$ 값을 살펴보면, $\alpha \lt 0$ 인 경우가 꽤 많다는 사실을 알 수 있다. 즉 가격모멘텀 $\mathbf{R}_i$ 이 클 수록 투자비중을 낮추는 경우가 많았다는 의미이다.

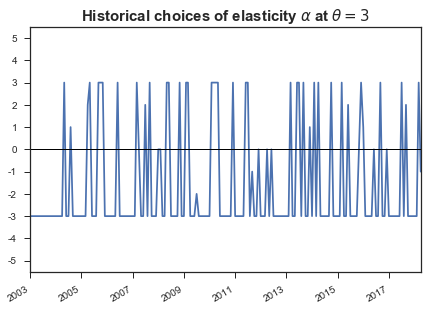
이는 굉장히 신선한 결과였다. (백테스트 결과가 맞다는 가정하에) 가격모멘텀 $\mathbf{R}_i$ 의 크기를 기준으로 자산을 선택하되, 가격모멘텀이 1등인 자산보다는 2등-3등의 비중을 더 높이는 의사결정이 상대적으로 유리한 경우가 많았다는 의미로 해석된다.

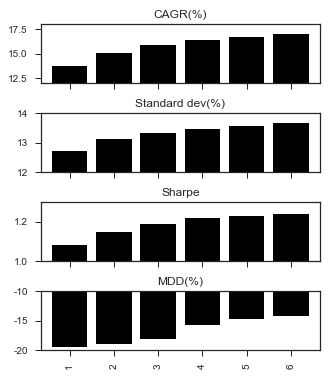
다음은 $\theta$ 값에 따른 백테스트 누적수익률 및 단일자산 쏠림현상을 보여준다.

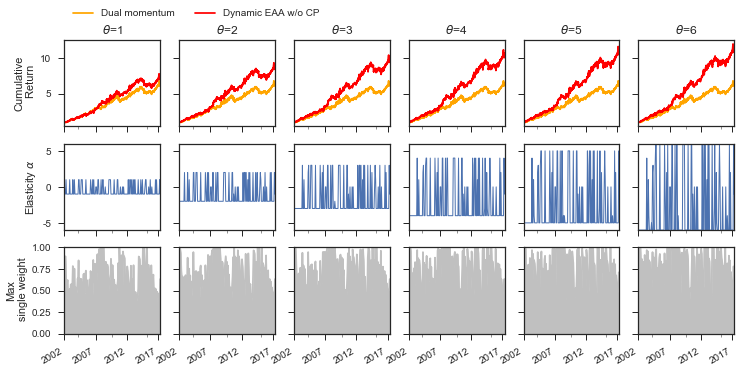
재미있는 사실은, $\theta$ 가 커질 수록 특정자산에의 비중 쏠림현상이 심해진 것은 사실이나, Sharpe는 더 커졌고, MDD는 오히려 더 작아졌다는 것이다.

이제 마지막으로, Crash protection까지 모두 반영한 백테스트 결과를 확인해보자. 동등한 비교를 위해, Dual momentum에도 Crash protection을 같이 반영해보았다. $\theta=2$ 를 가정하였다.

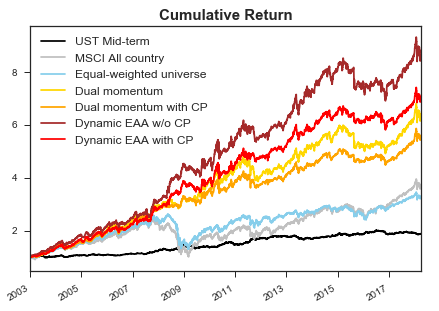
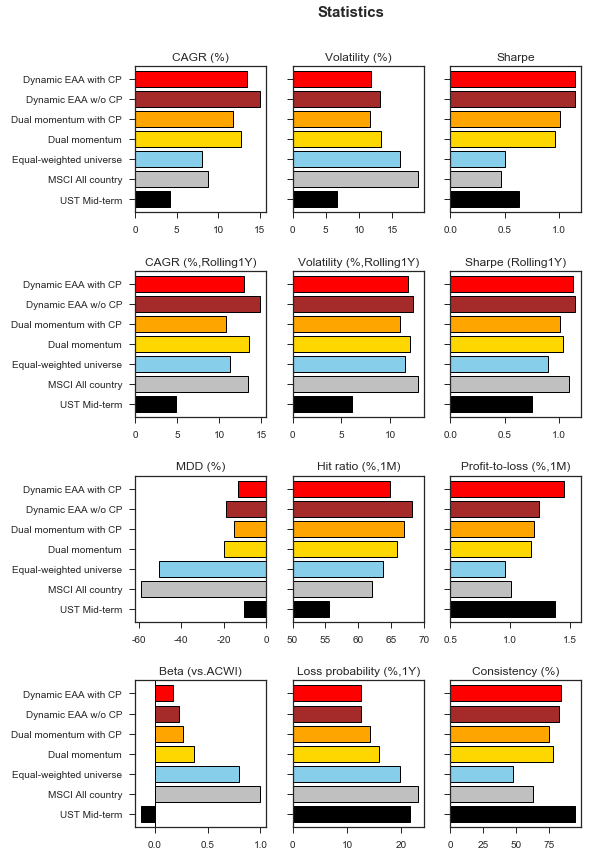
Crash protection을 통해 성과가 크게 개선되었다고 보기는 힘들었다. CAGR가 변동성은 모두 조금씩 축소되었고, Sharpe은 유사한 수준으로 유지되었다.
다만 MDD와 시장베타(vs ACWI) 값은 소폭 낮아지는 효과는 확인할 수 있었다. 단 기대했던 수준은 아니었다.

Conclusions

Dual momentum 전략을 개선하고자 하는 의도에서 Keller 교수의 EAA 전략을 검토해보았다. EAA에서는 애초에 자산간 상관계수를 고려하여 자산을 선택하는 프로세스가 포함되어 있기 때문에, 투자 안정성 측면에서는 양호한 전략일 수 있으나, 수익률 측면에서 Dual momentum을 이기긴 힘들었다. 이에, 논문의 전략을 일부 수정하였다. 즉

(모멘텀 스코어가 아닌) 가격모멘텀을 기준으로 자산선택
총 모멘텀을 극대화 하는 방향으로 매 리밸런싱마다 EAA 모형을 재정의

이를 통해 CAGR과 Sharpe 측면에서 Dual momentum 보다 나아보이는 전략을 수립할 수 있었다. 특히 선택된 자산의 비중을 결정하는 단계에서, 모멘텀 스코어가 2-3등인 자산의 비중을 높이는 것이 의외로 효과가 좋았던 점은 재미있는 현상이었다. 단, Crash protection의 효과는 생각보다 크지 않았다.

물론 이는 지극히 개인적인 의견에 불과하다. 해당 고민을 단번에 해결해줄 수 있는 굉장히 훌륭한 모멘텀 전략이 존재할 수도 있으며, 아직 그런 전략을 찾지 못했다고 말하는 게 좀더 정확한 표현일 것이다. ↩
다른 논문들에서의 실험에 의하면, 12개월 이내의 수익률과 미래의 수익률은 (+)의 상관관계가 있다(즉 예측력이 있다)고 알려져있다. 반면 12개월 이상의 긴 수익률은 Mean-reverting 가능성이 높다고 한다. Asness의 논문(2012) 참고. ↩
여러 구간의 수익률을 조합하여 가격모멘텀 지표로 활용하는 것은 꾸준히 시도되어 왔다. Faber의 논문(2010)과 Hurst의 논문(2012)을 참고. ↩
Elasticity라고 불리는 이유는, $\mathbf{R}_i$ , $\mathbf{C}_i$ , $\mathbf{V}_i$ 값의 변화에 대해 $z_i$ 가 얼마나 탄력적으로 변동하는 지를 결정하는 상수이기 때문인 것으로 보인다. 한편, 논문의 Notation과 다르므로 유의하기 바란다. 논문에서는 $\alpha, \beta, \gamma$ 가 아니라 $wR, wC, wV$ 라고 표기하였다. 취향의 차이임을 밝힌다. ↩
Without Loss of Generality (WLOG) ↩
MDD를 $x$ 축에, CAGR을 $y$ 축에 그려넣는다. Risk-Return profile과 같은 개념이라고 생각하면 된다. ↩

Written on July 9th, 2018 by quanty

Feel free to share!