정보이론의 기초

정보이론의 기초적인 문법을 정리한다. 정보의 의미와 엔트로피의 정의, KL 다이버전스 등에 대해 살펴본다. 차후에 다루게 될 머신러닝 관련 포스트에서, 수식전개를 돕기 위해 쓰이게 될 것이다.

정보
엔트로피
- 예시: 동전 던지기
- 주요성질
결합 엔트로피
교차 엔트로피
조건부 엔트로피
- Chain rule
- 정보이득
KL 다이버전스
- Information inequality
- 예시

정보

정보는 갖고 싶을 만한 가치를 지니고 있어야 한다. 마음만 먹으면 누구라도 가질 수 있거나, 너무 자주 발생해서 쉽게 알아낼 수 있다면, 그건 좋은 정보라고 말할 수 없을 것이다. 혹자는 정보를 놀람의 크기(Surprising degree) 또는 파급력 정도로 이해하기도 한다. 예를들어 내일은 추울수도 있고 더울수도 있다라는 식의 당연한 얘기는, 정보로서의 효용이 크다고 말하기는 힘들다. 하지만 내일부터 장마가 시작된다라는 일기예보는 누가 듣더라도 가치있는 정보가 된다.

정보이론(Information theory)에 따르면 정보량 $\mathbf{I}(\cdot): \mathbb{R} \mapsto \mathbb{R}$ 은 발생확률 $p$ $(0 \le p \le 1)$ 의 함수이며, 다음의 4가지 성질을 지니고 있다고 한다.

발생확률이 작을 수록 더 많은 정보량을 갖고 있다:

$p_i \ge p_j \Longrightarrow \mathbf{I}(p_i) \le \mathbf{I}(p_j)$

정보량은 음이 아니다:

$\mathbf{I}(p) \ge 0$

반드시 발생하는 사건(deterministic event)의 정보량은 0이다. (즉 정보가치가 없다)

$\mathbf{I}(1) = 0$

독립인 사건들의 정보량은 단순합산(additive)할 수 있다.

$\mathbf{I}(p_i p_j) = \mathbf{I}(p_i) + \mathbf{I}(p_j)$

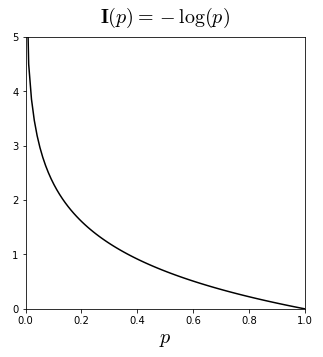
여기서 정보량 $\mathbf{I}$ 는 self-information 또는 surprisal 이라고도 부른다. 섀넌은 위의 성질들을 모두 만족하는 로그함수를 이용하여, 다음과 같이 정보량을 정의하였다.

$\mathbf{I}(p) \equiv \log (1/p) = -\log p$

정보이론에서는 기본 연산단위가 비트(bit)이기 때문에, 주로 이진로그( $\log_2$ )로 정보량을 정의한다. 이 때의 정보량 단위를 비트(bit) 또는 섀넌(shannon)이라고 한다. 예를들어 발생확률이 25%와 50%인 정보의 정보량을 각각 계산해보면,

$\begin{aligned} \mathbf{I}(0.25) &= \mathbf{I}(2^{-2})= - \log_2 2^{-2} = 2 ~\text{bit} \\ \mathbf{I}(0.50) &= \mathbf{I}(2^{-1})= - \log_2 2^{-1} = 1 ~\text{bit} \end{aligned}$

즉 발생확률이 낮을 수록 정보량이 더 크다. 참고로 머신러닝에서는 자연로그( $\ln$ )로 정보량을 정의하는 경우가 많은데, $\ln x$ 가 지수함수 $e^x$ 의 역함수일 뿐만 아니라 간편한 미분연산 등 대수적인 전개가 용이하기 때문이다. 이처럼 자연로그를 쓰는 경우의 정보량 단위를 내트(nat) 라고 한다. 정보량의 정의에 의해, $0 \le \mathbf{I}(p) \lt \infty$ 임을 알 수 있다.

엔트로피

엔트로피(Entropy)는 확률변수의 불확실성(Uncertainty)을 측정하는 도구 중의 하나이다. 원래는 고전 열역학에서 소개된 개념인데, 섀넌의 1948년 논문인 A Mathematical Theory of Communication을 통해 정보이론으로 접목되었다. 확률변수 $X$ 에 대하여, 엔트로피 $\mathbf{H} \in \mathbb{R}$ 는 정보량 $\mathbf{I}$ 의 기대값으로 정의된다.

$\mathbf{H}[X] \equiv \mathbf{E} [\mathbf{I}(p(X))] = -\mathbf{E}[\log p(X)] = \mathbf{H}(p)$

여기서 $p(x)$ 는 확률변수 $X$ 의 확률밀도함수를 의미하며, 엔트로피를 $p$ 의 함수로 이해하는 경우도 있기 때문에, 위의 정의처럼 $\mathbf{H}(p)$ 라고 표기하기도 한다. 한편 엔트로피의 단위는 정보량의 단위에 따라 달라진다. ¹

엔트로피는 정보의 불확실성이나, 해당 정보를 접했을 때 느끼는 평균적인 파급력(놀람)의 크기 정도로 해석한다. 왜냐하면 다음과 같은 추론이 가능하기 때문이다.

정보량의 기대값이 크면,
해당 정보에 대한 평균적인 파급력의 크기가 클 것이고,
이느 결과적으로 해당 정보의 불확실성이 크다는 것을 의미한다.

만약 확률변수 $X$ 가 베르누이 분포 또는 카테고리 분포 등의 이산확률분포를 따른다면, 엔트로피를 좀 더 명시적으로 나타낼 수 있다. 이를 섀넌 엔트로피(Shannon entropy) 또는 정보 엔트로피(Information entropy) 라고 부르기도 한다.² 이산확률변수 $X$ 의 표본공간(Sample space)³을 $\mathbb{X}$ 라고 하면, 섀넌 엔트로피는 다음과 같다.

$\mathbf{H}[X] = -\sum_{x \in \mathbb{X}} p(x) \log p(x)$

이 때 $p(\cdot)$ 는 확률질량함수가 된다.

Notation이 다소 헷갈릴 수도 있으니 정리하고 넘어가자. 다음의 설정들에 대해서,

이산확률변수 $X$ 의 표본공간 $\mathbb{X} = \{ x_1, \cdots, x_n \}$
$X$ 의 각 샘플 $x_i$ 에 할당된 확률값 $p_i \equiv p(x_i)$
$p_1 + \cdots + p_n = 1$

아래의 엔트로피 표현들은 모두 같은 의미를 지닌다.

$\mathbf{H}[X] = \mathbf{H}(p) = \mathbf{H}_n (p_1, \cdots, p_n) = - \sum_{i=1}^n p_i \log p_i$

표본공간의 크기가 $n$ 이라는 것을 표현하기 위해, 각 확률값 $p_i$ 의 함수로 나타내는 경우, $\mathbf{H}_n(\cdots)$ 과 같이 $n$ 을 명시적으로 표시하였다.

$p = 0$ 인 경우

이산확률변수 $X$ 에서 추출된 어떤 샘플의 발생확률이 $p=0$ 일 때에는, 해당 엔트로피의 계산에 $0 \log 0$ 이 포함되기 때문에, 엔트로피가 명확히 정의되지 않는다. 이 경우에는 다음을 정의하여 이용한다.

$\Bigl[ p \log p \Bigr]_{p = 0} \equiv \lim_{p \to 0+} p \log p$

로피탈의 정리(L’Hospital’s rule)에 의해,

$\lim_{p \to 0+} p \log p = \lim_{p \to 0+} \frac{(\log p)'}{(1/p)'} = \lim_{p \to 0+} \frac{1/p}{-1/p^2} = 0$

이므로, 발생확률이 0인 정보량은 엔트로피 계산에서 제외해도 상관없게 된다. 따라서 발생확률이 0이 아닌 표본공간 $\mathbb{X}_o$ $(\subset \mathbb{X})$ 에 대해서, 엔트로피는 다음과 같이 계산된다.

$\mathbf{H}[X] = -\sum_{x \in \mathbb{X}_o} p(x) \log p(x)$

예시: 동전 던지기

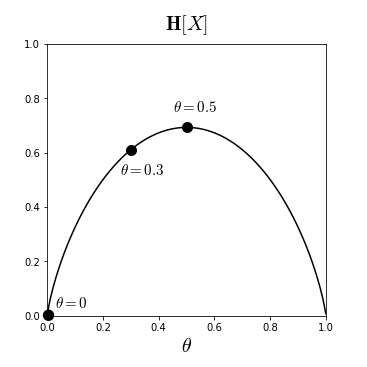
동전 던지기를 통해 엔트로피의 개념을 이해해보자. 동전 던지기의 확률변수 $X \in \{ 0, 1 \}$ 는 성공확률 $\theta \equiv \Pr[X=1] \in \mathbb{R}$ 의 베르누이 분포를 따른다. 확률질량함수 $p(x) = \mathbf{Bern}(x;\theta)$ 에 대하여, 자연로그로 정의된 엔트로피를 산출해보면,

$X \sim \mathbf{Bern}(\theta)$

$\begin{aligned} \mathbf{H}[X] &= -p(1) \ln p(1) - p(0) \ln p(0)\\ &= -\theta \ln \theta - (1-\theta) \ln (1-\theta) \end{aligned}$

이와 같이, 베르누이 분포의 엔트로피를 성공확률 $\theta$ 의 함수로 나타내는 것을 이진 엔트로피 함수 (Binary entropy function) 라고 부른다. ⁴

$\theta=0$ 인 경우:

$\mathbf{H}[X] = -0 \ln 0 - 1 \ln 1 = 0$

$\theta=0.3$ 인 경우:

$\mathbf{H}[X] = -0.3 \ln 0.3 - 0.7 \ln 0.7 \approx 0.61$

$\theta=0.5$ 인 경우:

$\mathbf{H}[X] = -0.5 \ln 0.5 - 0.5 \ln 0.5 \approx 0.69$

따라서 $\theta=0.5$ 에 가까울 수록 엔트로피가 커진다는 사실을 알 수 있다. 공정(fair)한 동전일 수록 불확실성이 커진다는 것을 의미하는데, 사실 이는 동전 던지기의 확률분포 뿐만이 아니라 다른 모든 확률분포에 대해서도 마찬가지로 적용이 된다. 0과 1 사이의 모든 $\theta$ 에 대해서 엔트로피를 그려보면 다음 차트를 얻는다.

주요성질

확률변수 $X \in \mathbb{X}$ 와 $Y \in \mathbb{Y}$ 가 다음과 같이 정의된 이산확률분포를 따른다고 가정해보자.

$\begin{aligned} \mathbb{X} = \{ x_1, \cdots, x_n \}, ~p_i = \Pr[X=x_i] \\ \mathbb{Y} = \{ y_1, \cdots, y_m \}, ~q_j = \Pr[Y=y_j] \end{aligned}$

Zero probability의 기여

확률이 0인 샘플은 엔트로피에 전혀 영향을 주지 못한다. $0 \log 0 = 0$ 으로 정의되기 때문이다. 위에서 [ $p=0$ 인 경우]를 참고.

$\mathbf{H}_{n+1}(p_1, \cdots, p_n, 0) = \mathbf{H}_{n}(p_1, \cdots, p_n)$

엔로피의 최대값

이산균등분포 (Discrete uniform distribution)일때 엔트로피가 최대값을 가진다.

$\mathbf{H}_{n}(p_1, \cdots, p_n) \le \mathbf{H}_n (\tfrac{1}{n}, \cdots, \tfrac{1}{n}) = \log n$

Proof. $\log$ 는 Strictly concave 함수이므로, Jensen 부등식에 의해 다음을 알 수 있다.

$\begin{aligned} \mathbf{H}_n (p_1, \cdots, p_n) &= \mathbf{H}[X] \\ &= -\mathbf{E}[\log p(X)] \\ &= \mathbf{E} \left[\log \left( \frac{1}{p(X)} \right) \right] \\ &\le \log \mathbf{E} \left[\frac{1}{p(X)} \right] \end{aligned}$

여기서 등호는 $\frac{1}{p(X)}$ 가 상수일 때, 즉 $p_1 = \cdots = p_n = \frac{1}{n}$ 인 경우에만 발생하므로,

$\begin{aligned} \mathbf{H}_n(\tfrac{1}{n}, \cdots, \tfrac{1}{n}) = \log \mathbf{E} \left[\frac{1}{p(X)} \right] = \log n \end{aligned}$

참고로, 연속확률분포의 (연속) 엔트로피가 최대가 되려면, 해당 확률분포가 가우시안 정규분포를 따라야 한다는 사실이 알려져있다. 여기를 참고.

독립분포의 엔트로피 가산성

$X$ 와 $Y$ 가 서로 독립적인 이산확률분포를 따른다면,

$\mathbf{H}[X,Y] = \mathbf{H}[X] + \mathbf{H}[Y]$

이는, 독립적인 불확실성은 가산된다는 의미로 이해할 수 있다.

Proof.

$\begin{aligned} \mathbf{H}[X,Y] &= \mathbf{H}_{nm}(p_1 q_1, \cdots, p_i q_j, \cdots, p_n q_m) \\ &= -\sum_{i,j} p_i q_j \log (p_i q_j) \\ &= -\sum_{i=1}^n\sum_{j=1}^m p_i q_j (\log p_i + \log q_j) \\ &= -\sum_{i=1}^n\sum_{j=1}^m (p_i q_j \log p_i + p_i q_j\log q_j) \\ &= -\sum_{j=1}^m q_j \left(\sum_{i=1}^n p_i \log p_i \right) - \sum_{i=1}^n p_i \left( \sum_{j=1}^m q_j\log q_j \right) \\ &= \mathbf{H}_n(p_1, \cdots, p_n) + \mathbf{H}_m(q_1, \cdots, q_m) \\ &= \mathbf{H}[X] + \mathbf{H}[Y] \end{aligned}$

균등분포의 엔트로피

균등분포의 경우, 표본공간의 크기가 클 수록 (즉 확률변수가 취할 수 있는 값의 수가 많을 수록) 엔트로피가 커진다.

$\mathbf{H}_n (\tfrac{1}{n}, \cdots, \tfrac{1}{n}) \le \mathbf{H}_{n+1} (\tfrac{1}{n+1}, \cdots, \tfrac{1}{n+1})$

이를테면 동전 던지기 보다 주사위 던지기의 엔트로피가 더 크다고 할 수 있다.

Proof.

$\mathbf{H}_n (\tfrac{1}{n}, \cdots, \tfrac{1}{n}) = \log n \le \log (n+1) = \mathbf{H}_{n+1} (\tfrac{1}{n+1}, \cdots, \tfrac{1}{n+1})$

결합 엔트로피

결합 엔트로피 (Joint entropy)는 결합확률분포 (Joint probability distribution)의 엔트로피를 말한다. 두 확률변수 $X, Y$ 의 결합확률변수 $(X,Y)$ 에 대한 결합 엔트로피는 다음과 같이 정의된다.

$\mathbf{H}[X,Y] \equiv -\mathbf{E} [\log p(X,Y)]$

여기서 $p(x,y)$ 는 결합확률변수의 임의의 샘플 $(x,y)$ 에 대한 확률밀도함수를 의미한다. 확장하여, 결합확률변수 $\mathbf{X} = (X_1, \cdots, X_n)$ 의 샘플 $\mathbf{x} = (x_1, \cdots, x_n)$ 에 대한 확률밀도함수를 $p(\mathbf{x})$ 라고 하면,

$\mathbf{H}[\mathbf{X}] \equiv -\mathbf{E} [\log p(\mathbf{X})]$

가 된다. 만약 각 확률변수 $X_i$ 가 모두 이산확률분포를 따른다면, $\mathbf{x}$ 가 취할 수 있는 모든 값에 대하여 다음과 같이 나타낼 수 있다.

$\mathbf{H}[\mathbf{X}] = - \sum_{\mathbf{x}} p(\mathbf{x}) \log p(\mathbf{x})$

교차 엔트로피

하나의 확률변수 $X$ 를 묘사하는 두 개의 확률분포 $p$ 와 $q$ 가 있다고 생각해보자. 현실에서는 이런 경우가 빈번하게 발생한다. 이를테면 확률변수 $X$ 의 분포를 모르고 있는 상태에서 확률밀도함수를 추정한다면, 해당 확률밀도함수의 추정된 형태는 여러가지가 될 수 있는 것이다. 이럴 때에는 다음과 같이 교차 엔트로피 (Cross entropy) $\mathbf{H}(p,q)$ 를 정의할 수 있다.

$\mathbf{H}(p,q) \equiv - \mathbf{E}_{p} [\log q(X)]$

여기서 $\mathbf{E}_p[\cdot]$ 는 $X$ 의 확률밀도함수가 $p$ 인 경우의 기대값을 의미한다. 로그 안밖의 확률밀도함수가 다르다는 점만 제외하고는, 기존의 엔트로피 정의와 거의 동일하다. 만약 확률변수 $X$ 가 이산확률분포를 따른다면, $X$ 의 표본공간 $\mathbb{X}$ 에 대해 다음과 같이 나타낼 수 있다.

$\mathbf{H}(p,q) = - \sum_{x \in \mathbb{X}} p(x) \log q(x)$

베르누이 분포를 예로 들어보자. 확률변수 $X$ 의 세 확률분포 $p$ , $q_1$ , $q_2$ 에 대한 성공확률 $\theta$ 를

$\begin{aligned} \theta_p &\equiv p(1) = 0.2 \\ \theta_{q_1} &\equiv q_1(1) = 0.3 \\ \theta_{q_2} &\equiv q_2(1) = 0.9 \end{aligned}$

라고 한다면,

$\begin{aligned} \mathbf{H}(p,q_1) &= -\theta_{p} \ln \theta_{q_1} - (1-\theta_{p}) \ln (1-\theta_{q_1}) \\ &= - (0.2 \times \ln 0.3) - (0.8 \times \ln 0.7) \\ &= 0.526 \end{aligned}$

$\begin{aligned} \mathbf{H}(p,q_2) &= -\theta_{p} \ln \theta_{q_2} - (1-\theta_{p}) \ln (1-\theta_{q_2}) \\ &= - (0.2 \times \ln 0.9) - (0.8 \times \ln 0.1) \\ &= 1.863 \end{aligned}$

두 확률분포가 유사할 수록 교차 엔트로피가 작아진다는 사실을 알 수 있다. 베르누이 분포에서 0과 1 사이의 모든 성공확률 $\theta_p$ , $\theta_q$ 에 대한 교차 엔트로피를 그려보면 다음 차트를 얻는다. 두 확률분포가 유사한 구간인 $\theta_p \approx \theta_q$ 부근(점선)에서 교차 엔트로피가 0에 가깝다는 것을 다시한번 확인할 수 있다.

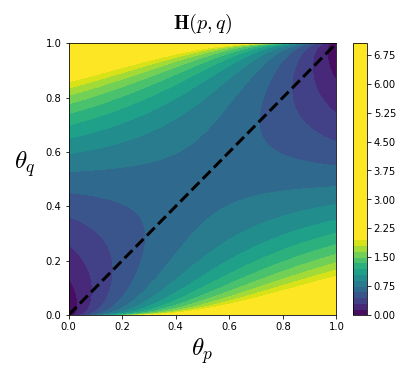
이와 같은 성질 때문에, 교차 엔트로피는 머신러닝의 분류 (Classification) 문제에서 비용함수 (Cost function)으로 쓰이는 경우가 많다. 위의 예를 다시한번 가져와 보자. $p$ 를 $X$ 의 실제 확률분포라고 하고, 해당 확률분포를 추정하여 $q_1$ 과 $q_2$ 를 얻게 되었다고 하자. 각 성공확률값에 따라 One-hot 인코딩을 통해 클래스를 분류해보면,

$\begin{aligned} p : (0.2, 0.8) &\xrightarrow{\text{One-hot }} p': (0, 1) = \color{red}{\text{class 2}}\\ q_1 : (0.3, 0.7) &\xrightarrow{\phantom{\text{One-hot }}} q_1': (0, 1) = \text{class 2}\\ q_2 : (0.9, 0.1) &\xrightarrow{\phantom{\text{One-hot }}} q_2': (1, 0) = \text{class 1} \end{aligned}$

여기서 $p', q_1', q_2'$ 는 One-hot 인코딩 과정을 통해 예상되는 클래스를 의미한다. $p$ 가 실제 분포라고 했으므로, 이 확률변수를 분류해보면 class 2가 틀림없을 것이다. 이제, 추정된 분포 $q_1$ 과 $q_2$ 를 통해 인코딩된 분류를, 교차 엔트로피를 이용하여 검증해보자.

$\begin{aligned} \mathbf{H}(p',q_1') &= -0 \ln 0 - 1 \ln 1 = 0 \\ \mathbf{H}(p',q_2') &= -0 \ln 1 - 1 \ln 0 = \infty \\ \end{aligned}$

즉, 잘못된 분류를 도출하는 분포의 경우에는 교차 엔트로피가 무한대로 발산하게 된다.

조건부 엔트로피

두 확률변수 $X, Y$ 가 서로 상관관계가 있을 때, 확률변수 $X$ 의 실현값 $x$ 를 조건으로 확률변수 $Y$ 의 엔트로피를 구해보면 $\mathbf{H}[Y|X=x]$ 가 된다. 이 값의 $X$ 에 대한 기대값을 조건부 엔트로피 (Conditional entropy) ⁵라고 하며, 다음과 같이 정의된다.

$\mathbf{H}[Y | X] \equiv \mathbf{E}_{X} \bigl[ \mathbf{H}[Y | X=x] \bigr]$

여기서 $\mathbf{E}_X [\cdot]$ 은 확률변수 $X$ 에 대한 기대값을 의미한다. 만약 확률변수 $X$ , $Y$ 가 이산확률분포를 따른다면, 조건부 확률 및 엔트로피의 정의에 의해 다음과 같이 전개할 수 있다.

$\begin{aligned} \mathbf{H}[Y | X] &= \sum_x p(x) ~\mathbf{H}[Y | x] \\ &= -\sum_x p(x) ~\sum_y p(y | x) \log p(y | x)\\ &= -\sum_{x,y} p(x) ~p(y | x) \log p(y | x)\\ &= -\sum_{x,y} p(x,y) \log p(y | x) \end{aligned}$

여기서 $p(x)$ , $p(y|x)$ , $p(x,y)$ 는 각각 확률변수 $X$ , $Y|X$ , $(X,Y)$ 의 확률질량함수를 의미한다. 결합 엔트로피 $\mathbf{H}[X,Y]$ $= -\mathbf{E} [\log p(X,Y)]$ $= -\sum_{x,y} p(x,y) \log p(x,y)$ 와 헷갈릴 수 있으므로, 주의하기 바란다.

Chain rule

조건부 엔트로피는 다음과 같은 재미있는 성질이 있는데, 이를 Chain rule ⁶이라고 부른다.

$\mathbf{H}[Y | X] = \mathbf{H}[X,Y] - \mathbf{H}[X]$

증명해보자.

$\begin{aligned} \mathbf{H}[Y | X] &= -\sum_{x,y} p(x,y) \log p(y | x) \\ &= -\sum_{x,y} p(x,y) \log \frac{p(x,y)}{p(x)} \\ &= -\sum_{x,y} p(x,y) \log p(x,y) + \sum_{x,y} p(x,y) \log p(x) \end{aligned}$

여기서

$\begin{aligned} -\sum_{x,y} p(x,y) \log p(x,y) &= \mathbf{H}[X,Y] \\ \sum_{x,y} p(x,y) \log p(x) &= \sum_x \left( \sum_y p(x,y) \right) \log p(x) \\ &= \sum_x p(x) \log p(x) \\ &= -\mathbf{H}[X] \end{aligned}$

임을 이용하면 증명이 완성된다. Chain rule을 활용하면 다음을 추가적으로 알 수 있다.

$\mathbf{H}[X,Y] = \mathbf{H}[Y | X] + \mathbf{H}[X] = \mathbf{H}[X | Y] + \mathbf{H}[Y]$

엔트로피 Chain rule의 일반형

Chain rule을 보다 일반적으로 기술하면 다음과 같다.

$\begin{aligned} \mathbf{H}[X_1, \cdots, X_n] &= \sum_{i=1}^n \mathbf{H}[X_i \mid X_1, \cdots, X_{i-1}] \end{aligned}$

증명은 간단하다. 다음 식들을 모두 합산해보면 위의 식을 얻게 된다.

$\begin{aligned} \mathbf{H}[X_n \mid X_1, \cdots, X_{n-1}] &= \mathbf{H}[X_1, \cdots, X_n] - \mathbf{H}[X_1, \cdots, X_{n-1}] \\ \mathbf{H}[X_{n-1} \mid X_1, \cdots, X_{n-2}] &= \mathbf{H}[X_1, \cdots, X_{n-1}] - \mathbf{H}[X_1, \cdots, X_{n-2}] \\ &~~\vdots \\ \mathbf{H}[X_{2} \mid X_1] &= \mathbf{H}[X_1, X_{2}] - \mathbf{H}[X_1] \\ \mathbf{H}[X_{1}] &= \mathbf{H}[X_1] \\ \end{aligned}$

정보이득

정보이득(Information Gain)은 주어진 정보로 인해 확률변수의 불확실성이 얼마나 감소했는지를 나타내는 지표이다. 정보이득 $\mathbf{IG}$ 는 다음과 같이 정의된다.

$\mathbf{IG}[Y, X] \equiv \mathbf{H}[Y] - \mathbf{H}[Y | X]$

KL 다이버전스

KL 다이버전스 (KLD: Kullback–Leibler divergence, 쿨백-라이블러 발산)는 하나의 확률변수에 대한 두 확률분포 간의 차이를 측정하는 도구 중 하나이며, 상대 엔트로피(Relative entropy) 라고도 한다. 확률분포 $p$ 와 $q$ 에 대하여, 다음과 같이 엔트로피와 교차 엔트로피 간의 차이로 정의된다.

$\mathbf{D}_{\text{KL}} (p \parallel q) \equiv \mathbf{H}(p,q) - \mathbf{H}(p)$

수학적인 의미는, 어떤 확률분포 $p$ 가 있을 때, 그 분포를 근사적으로 추정한 확률분포 $q$ 를 대신 사용했을 경우의 엔트로피 변화를 말한다. 엔트로피와 교차 엔트로피의 정의에 의해,

$\mathbf{D}_{\text{KL}} (p \parallel q) = \mathbf{E}_p \left[ \log p(X) - \log q(X) \right]$

임을 알 수 있다. 만약 $X$ 가 이산확률변수이고, 표본공간 $\mathbb{X}= \{ x_1, \cdots, x_n \}$ 에 대하여 $p_i = p(x_i)$ 및 $q_i = q(x_i)$ 이라면, 가장 널리 알려진 다음의 정의를 얻게 된다.

$\mathbf{D}_{\text{KL}} (p \parallel q) = \sum_{i=1}^n p_i \log \frac{p_i}{q_i}$

한편, KL 다이버전스를 두 확률분포 간의 거리 개념으로 이해할 수도 있다. 단 Symmetric 하지는 않다는 점을 명심해야 한다. 즉,

$\mathbf{D}_{\text{KL}} (p \parallel q) \ne \mathbf{D}_{\text{KL}} (q \parallel p)$

Information inequality

$X$ 의 두 확률밀도함수 $p, q$ 에 대해서, 다음의 부등식을 Information inequality 라고 한다.

$\mathbf{D}_{\text{KL}} (p \parallel q) \ge 0$

$\mathbf{D}_{\text{KL}} (p \parallel q) = 0 \Longleftrightarrow p(x)=q(x)$

Information inequality를 이용하면, KL 다이버전스의 정의에 의해 다음의 부등식을 추가적으로 알게 된다.

$\mathbf{H}(p,q) \ge \mathbf{H}(p)$

Proof. $\log$ 는 Strictly concave 함수이므로, Jensen 부등식을 이용하면,

$\begin{aligned} \mathbf{D}_{\text{KL}} (p \parallel q) &= -\mathbf{E}_p \left[ \log \frac{q(X)}{p(X)} \right] \\ &\ge -\log \mathbf{E}_p \left[ \frac{q(X)}{p(X)} \right] \\ &= -\log \left(\sum_x p(x) \frac{q(x)}{p(x)} \right) \\ &= -\log 1 \\ &= 0 \end{aligned}$

여기서는 $X$ 가 이산확률변수라고 가정하였는데, 연속확률변수인 경우에도 같은 논리를 적용할 수 있다. 이를테면 $\mathbf{E}_p \left[ \frac{q(X)}{p(X)} \right] = \int_x p(x) \frac{q(x)}{p(x)}dx = \int_x q(x) dx = 1$ 이므로, 결국 위와 동일한 부등식을 얻을 수 있게 된다.

한편 등호는 $\frac{q(X)}{p(X)}$ 가 상수일 때 성립한다. $\frac{q(X)}{p(X)} = c$ 에서

$1 = \sum_x q(x) = c \sum_x p(x) = c$

따라서 모든 $x$ 값에 대하여 $p(x) = q(x)$ 가 된다.

다음 차트는 다양한 위치의 두 정규분포에 대하여 KL 다이버전스를 측정해 본 결과이다.

(출처: http://yusuke-ujitoko.hatenablog.com)

예시

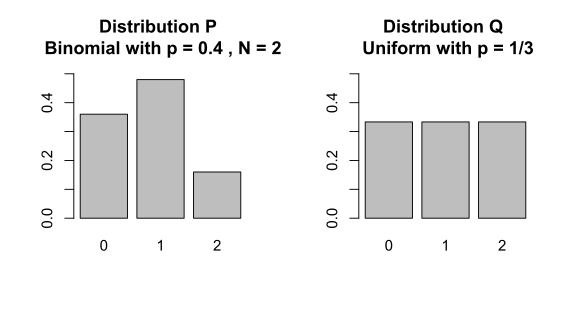
아래 표에서 $P$ 는 이항분포(Binomial distribution), $Q$ 는 균등분포(Uniform distribution)을 나타낸다.

	1	2	3
$P$	0.36	0.48	0.16
$Q$	0.333	0.333	0.333

(출처: 위키피디아)

$\begin{aligned} \mathbf{D}_{\text{KL}}(P \parallel Q) &= \sum_i P(i) \ln \tfrac{P(i)}{Q(i)} \\ &= 0.36 \ln \tfrac{0.36}{0.333} + 0.48 \ln \tfrac{0.48}{0.333} + 0.16 \ln \tfrac{0.16}{0.333} \\ &= 0.0853 \\[6pt] \mathbf{D}_{\text{KL}}(Q \parallel P) &= \sum_i Q(i) \ln \tfrac{Q(i)}{P(i)} \\ &= 0.333 \ln \tfrac{0.333}{0.36} + 0.333 \ln \tfrac{0.333}{0.48} + 0.333 \ln \tfrac{0.333}{0.16} \\ &= 0.0975 \end{aligned}$

만약 정보량의 단위가 비트라면(즉 정보량을 이진로그로 정의한다면) 엔트로피의 단위도 비트가 된다. 반대로 정보량의 단위가 내트라면(즉 정보량을 자연로그로 정의한다면) 엔트로피의 단위 역시 내트가 된다. ↩
이와는 반대 개념으로, 연속확률변수에 대한 엔트로피를 연속 엔트로피(Continuous entropy or Differential entropy) 라고 하며, 다음과 같이 정의된다. $\mathbf{H}[X] = -\int_{x \in \mathbb{X}} p(x) \log p(x) ~dx$ ↩
확률변수 $X$ 가 취할 수 있는 모든 값의 범위를 뜻한다. 여기를 참고. ↩
보통은 이진로그로 정의하는 경우가 많으나, 여기에서는 자연로그를 썼다. ↩
조건부 불확실성 또는 Equivocation 라고도 부른다. ↩
수학에는 굉장히 다양한 종류의 Chain rule 들이 존재한다. 여기와 여기를 참고. ↩

Written on August 16th, 2018 by quanty

Feel free to share!