Affinity와 Convexity

Affinity와 Convexity는 머신러닝에서 최적화 (Optimization)의 논리적인 근거를 제공하는 핵심개념이다. Convexity에서 파생되는 Jensen 부등식도 같이 알아본다.

Affine set과 Convex set convex_fn

Affinity
Convexity
Convex + Concave = Affine map
Jesen 부등식

Affinity

Affine combination

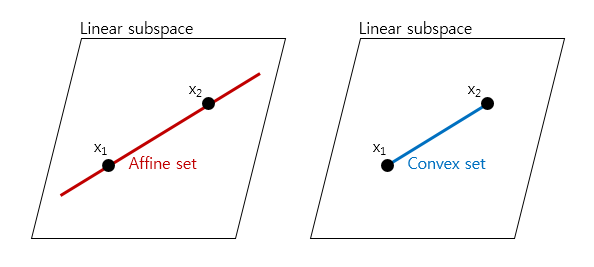
유한 개의 벡터들로 선형결합 (Linear combination)을 할 때, 모든 계수(coefficient)들의 합이 1인 경우를 Affine combination이라고 한다. $r$ 개의 벡터 $\mathbf{x}_1, \cdots, \mathbf{x}_r$ 에 대해서, Affine combination은 다음과 같이 표현된다.

$\lambda_1 \mathbf{x}_1 + \cdots + \lambda_r \mathbf{x}_r$

여기서 실수 $\lambda_i$ 는 $\lambda_1 + \cdots + \lambda_r = 1$ 을 만족한다. 유클리드 공간(Euclidean space)에서 임의의 두 점을 선택했을 때, 두 점을 지나는 직선 상의 모든 점들은 Affine combination으로 표현할 수 있다.

Affine set

Affine combination에 대해서 닫혀있는(closed) 집합을 Affine set 이라고 한다. 만약 집합 $\mathbb{A}$ 가 Affine set 이라면, 이 집합에서 $r$ 개의 원소 $\mathbf{x}_1, \cdots, \mathbf{x}_r \in \mathbb{A}$ 를 임의로 추출했을 때, 해당 원소들의 Affine combination도 $\mathbb{A}$ 에 속하게 된다. 즉 $\lambda_1 + \cdots + \lambda_r = 1$ 에 대해서,

$\lambda_1 \mathbf{x}_1 + \cdots + \lambda_r \mathbf{x}_r \in \mathbb{A}$

Affine map

Affine map¹이란 Linear map²과 Translation³이 결합된 형태의 좌표변환을 말한다.

Affine map = Linear map + Translation

구체적으로 기술하자면, Affine set $\mathbb{A} \subset \mathbb{R}^n$ 의 원소 $\mathbf{x} \in \mathbb{A}$ 와 벡터 $\mathbf{b} \in \mathbb{R}^m$ 및 행렬 $\mathbf{A} \in \mathbb{R}^{n \times m}$ 에 대해서 다음과 같은 형태의 함수 $h(\cdot):\mathbb{A} \mapsto \mathbb{R}^m$ 를 의미한다.

$h(\mathbf{x}) = \mathbf{A}^\mathsf{T} \mathbf{x} + \mathbf{b}$

위의 Affine map은 좀더 간편한 형태로 변환할 수 있다.

$\begin{bmatrix} h(\mathbf{x}) \\ 1 \end{bmatrix} = \underbrace{\begin{bmatrix} \mathbf{A}^\mathsf{T} & \mathbf{b} \\ 0 & 1 \end{bmatrix}}_{\mathbf{M}} \begin{bmatrix} \mathbf{x} \\ 1 \end{bmatrix}$

여기서 행렬 $\mathbf{M} \in \mathbb{R}^{(m+1) \times (n+1)}$ 을 Augmented matrix 라고 한다. 다음은 여러가지 형태의 Augmented matrix $\mathbf{M}$ 에 따른 Affine map을 보여준다.

(출처: 위키피디아)

Convexity

Convex combination

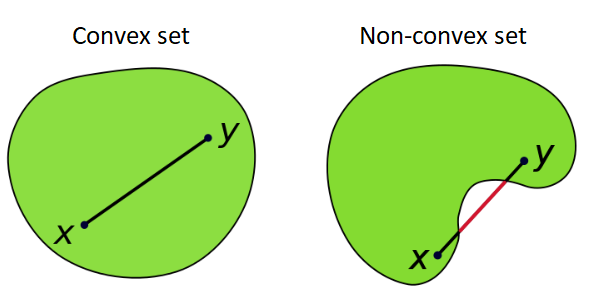
Affine combination에서 모든 계수들이 0 이상이라는 추가적인 제약조건이 있는 경우를 Convex combination 이라고 한다. $r$ 개의 벡터 $\mathbf{x}_1, \cdots, \mathbf{x}_r$ 에 대해서, Convex combination은 다음과 같이 표현된다.

$\lambda_1 \mathbf{x}_1 + \cdots + \lambda_r \mathbf{x}_r$

여기서 실수 $\lambda_i$ 는 $\lambda_i \ge 0$ 과 $\lambda_1 + \cdots + \lambda_r = 1$ 을 만족한다. 유클리드 공간에서 임의의 두 점을 선택했을 때, 두 점을 잇는 직선 사이의 모든 점들은 Convex combination으로 표현할 수 있다.

Convex set

Convex combination에 대해서 닫혀있는 집합을 Convex set 이라고 한다. 만약 집합 $\mathbb{S}$ 가 Convex set 이라면, 이 집합에서 $r$ 개의 원소 $\mathbf{x}_1, \cdots, \mathbf{x}_r \in \mathbb{S}$ 를 임의로 추출했을 때, 해당 원소들의 Convex combination도 $\mathbb{S}$ 에 속하게 된다. 즉 $\lambda_i \ge 0$ 및 $\lambda_1 + \cdots + \lambda_r = 1$ 에 대하여,

$\lambda_1 \mathbf{x}_1 + \cdots + \lambda_r \mathbf{x}_r \in \mathbb{S}$

정의에 의해, 모든 Affine set은 Convex set 이라고 할 수 있다.

(출처: 위키피디아)

Convex function

Convex set $\mathbb{S}$ 에서 추출된 원소들 $\mathbf{x}_1, \mathbf{x}_2 \in \mathbb{S}$ 와 실수 $\lambda \in [0, 1]$ 에 대하여, 함수 $f(\cdot): \mathbb{S} \mapsto \mathbb{R}$ 가 다음의 부등식을 만족할 때, 이 함수를 Convex function이라고 부른다.

$f \bigl( \lambda \mathbf{x}_1 + (1-\lambda)\mathbf{x}_2 \bigr) \le \lambda f(\mathbf{x}_1) + (1-\lambda) f(\mathbf{x}_2)$

쉽게 말해서 Convex function은 아래로 볼록 함수를 일컫는다. 다음 차트를 보면, $\mathbb{S} = [a,b] \subset \mathbb{R}$ 인 경우에 대해 직관적으로 이해할 수 있을 것이다.

Convex function의 형태 convex_fn

(출처: https://am207.github.io)

만약 $-f$ 가 Convex function이라면, 이 경우의 함수 $f$ 를 Concave function (위로 볼록 함수)이라고 부른다.

Strictly convex function

모든 $\mathbf{x}_1 \ne \mathbf{x}_2 \in \mathbb{S}$ 와 $\lambda \in (0, 1)$ 에 대하여 다음의 부등식이 성립하는 경우, 이 함수 $f(\cdot): \mathbb{S} \mapsto \mathbb{R}$ 를 Strictly convex function 이라고 한다.

$f \bigl( \lambda \mathbf{x}_1 + (1-\lambda)\mathbf{x}_2 \bigr) \lt \lambda f(\mathbf{x}_1) + (1-\lambda) f(\mathbf{x}_2)$

참고로 Affine function은 Strictly convex function에 포함되지 않는다. 만약 $f$ 가 affine function 이라면, $\mathbf{x}_1 \ne \mathbf{x}_2$ 에 대해서 윗식의 등호가 성립하며, 이는 Strictly convex function의 정의에 어긋나게 된다. 따라서 Strictly convex function은, Convex function 중 선형(Linear)인 구간이 전혀 없는 함수로 이해할 수 있다. 만약 $-f$ 가 Strictly convex function이라면, 이 경우의 함수 $f$ 를 Strictly concave function 이라고 부른다.

비교: Combinations and Sets

유한 개의 벡터 $\mathbf{x}_1, \cdots, \mathbf{x}_r$ 와 $\lambda_i \in \mathbb{R}$ 에 대하여 Affine combination과 Convex combination은 다음과 같이 선형결합(Linear combination)으로 나타낼 수 있다.

$\lambda_1 \mathbf{x}_1 + \cdots + \lambda_r \mathbf{x}_r$

단 제약조건이 다르다.

Affine combination Convex combination

$\sum_{i=1}^r \lambda_i = 1$ $\sum_{i=1}^r \lambda_i = 1, ~\lambda_i \in [0,1]$

Affine set과 Convex set은 각각 Affine combination과 Convex combination에 닫혀있는 공간을 의미한다. 임의의 원소 $\mathbf{x}_1, \mathbf{x}_2$ 가 포함되어 있는 최소한의 Affine set과 Convex set을 구성해보면 다음 그림과 같다. ⁴

참고로 Linear subspace란, 제약조건이 없는 모든 선형결합에 대해서 닫혀있는 공간을 뜻한다.

Affine combination	Convex combination
$\sum_{i=1}^r \lambda_i = 1$	$\sum_{i=1}^r \lambda_i = 1, ~\lambda_i \in [0,1]$

Convex + Concave = Affine map

어떤 함수가 아래로 볼록(convex)이면서 동시에 위로 볼록(concave)이라면, 직관적으로 이 함수는 선형함수일 것으로 예상된다. 보다 명확하게 서술하면 다음과 같다.

Affine set $\mathbb{A} \subset \mathbb{R}^n$ 에서 정의된 함수 $f(\cdot): \mathbb{A} \mapsto \mathbb{R}$ 에 대하여,

$(f: \textsf{Affine}) ~\Longleftrightarrow~ (f: \mathsf{Convex ~\&~ Concave})$

Proof.

$(1)\Rightarrow$

함수 $f$ 가 Affine map 이라고 하자. 정의에 의해, 벡터 $\mathbf{a} \in \mathbb{R}^n$ 과 상수 $b \in \mathbb{R}$ 에 대하여 $f(\mathbf{x}) = \mathbf{a}^\mathsf{T} \mathbf{x} + b$ 로 나타낼 수 있다. Affine set $\mathbb{A}$ 는 Convex set이므로, $\mathbf{x}_1, \mathbf{x}_2 \in \mathbb{A}$ 및 $\lambda \in [0,1]$ 에 대하여,

$\begin{aligned} f \left( \mathbf{\lambda \mathbf{x}_1} + (1-\lambda) \mathbf{x}_2 \right) &= \mathbf{a}^\mathsf{T} \left( \mathbf{\lambda \mathbf{x}_1} + (1-\lambda) \mathbf{x}_2 \right) + b \\ &= \lambda (\mathbf{a}^\mathsf{T} \mathbf{x}_1 + b) + (1-\lambda) (\mathbf{a}^\mathsf{T} \mathbf{x}_2 + b) \\ &= \lambda f(\mathbf{x}_1) + (1-\lambda) f(\mathbf{x}_2) \end{aligned}$

즉 다음 두 개의 부등식,

$\begin{aligned} f \bigl( \lambda \mathbf{x}_1 + (1-\lambda)\mathbf{x}_2 \bigr) &\le \lambda f(\mathbf{x}_1) + (1-\lambda) f(\mathbf{x}_2) \\ f \bigl( \lambda \mathbf{x}_1 + (1-\lambda)\mathbf{x}_2 \bigr) &\ge \lambda f(\mathbf{x}_1) + (1-\lambda) f(\mathbf{x}_2) \end{aligned}$

을 동시에 만족하게 되고, 따라서 함수 $f$ 는 Affine set $\mathbb{A}$ 에서 Convex 및 Concave 하게 된다.

$(2)\Leftarrow$

함수 $f$ 가 Convex & Concave 하다고 가정하자. $f$ 를 Affine map 의 형태로 유도하면 증명이 완성된다. 그런데 한 가지 문제가 있다. 아래의 증명을 전개하는 과정에서 Affine set $\mathbb{A}$ 가 반드시 원점을 포함해야 한다는 논리가 필요한데, 그렇다는 보장이 없다. 좌표변환을 통해, 원점을 포함하는 Affine set $\mathbb{A}_o$ 를 새롭게 정의해보자.

임의의 $\alpha \in \mathbb{A}$ 에 대하여, Affine set $\mathbb{A}$ 전체를 $-\alpha$ 만큼 좌표변환한 집합 $\mathbb{A}_o$ 을 다음과 같이 정의하면,

$\mathbb{A}_o = \{ \mathbf{x} - \alpha \mid \mathbf{x} \in \mathbb{A} \} \ni 0$

$\mathbb{A}_o$ 는 원점을 포함하게 된다. 과연 $\mathbb{A}_o$ 는 Affine set 일까? 임의의 $\mathbf{z}_i \in \mathbb{A}_o$ 및 $\theta_1 + \cdots + \theta_r = 1$ 에 대하여,

$\begin{aligned} \mathbf{x}_i \equiv \mathbf{z}_i + \alpha &\in \mathbb{A} \\ \theta_1 \mathbf{x}_1 + \cdots + \theta_r \mathbf{x}_r \overset{\text{let}}{=} \mathbf{y} &\in \mathbb{A} \end{aligned}$

라고 하면,

$\begin{aligned} \theta_1 \mathbf{z}_1 + \cdots + \theta_r \mathbf{z}_r &= \sum_{i=1}^r \theta_i (\mathbf{x}_i - \alpha) \\ &= \sum_{i=1}^r \theta_i \mathbf{x}_i - \alpha \\ &= \mathbf{y} - \alpha \in \mathbb{A}_o \end{aligned}$

따라서 $\mathbb{A}_o$ 는 원점을 지나는 Affine set 이라고 할 수 있다. 이제 $\mathbb{A}_o$ 에서 정의된 함수 $g(\cdot): \mathbb{A}_o \mapsto \mathbb{R}$ 를 다음과 같이 새로 정의한다.

$g(\mathbf{z}) \equiv f(\mathbf{z+\alpha}) - f(\alpha)$

여기서 $g(0)$ $= 0$ 임을 알 수 있다. 함수 $g$ 은 다음의 세 가지 특성을 가지고 있는데, 이들을 추가적으로 증명해보자.

[Convex & Concave] $f$ 와 마찬가지로, $g$ 는 Convex & Concave 하다
[Multiplication] 모든 $\mathbf{z} \in \mathbb{A}_o$ 와 실수 $\gamma \ge 0$ 에 대하여, $g(\gamma \mathbf{z}) = \gamma g(\mathbf{z})$
[Additivity] $\mathbf{z}_1, \mathbf{z}_2 \in \mathbb{A}_o$ 에 대하여, $g(\mathbf{z}_1 + \mathbf{z}_2) = g(\mathbf{z}_1) + g(\mathbf{z}_2)$

1. Convex & Concave

가정에 의해 함수 $f$ 가 Convex & Concave 하므로, $\mathbf{z}_1, \mathbf{z}_2 \in \mathbb{A}_o$ 및 $k \in \mathbb{R}$ 에 대하여,

$\begin{aligned} g &\left( k \mathbf{z}_1 + (1-k) \mathbf{z}_2 \right) \\ &= f \left( k \mathbf{z}_1 + (1-k) \mathbf{z}_2 + \alpha \right) - f(\alpha) \\ &= f \left( k (\mathbf{z}_1 + \alpha) + (1-k) (\mathbf{z}_2 + \alpha) \right) - f(\alpha) \\ &= k f (\mathbf{z}_1 + \alpha) + (1-k) f(\mathbf{z}_2 + \alpha) - f(\alpha) \\ &= k \left( g(\mathbf{z}_1) + f(\alpha) \right) + (1-k) \left( g(\mathbf{z}_2) + f(\alpha) \right) - f(\alpha) \\ &= k g(\mathbf{z}_1) + (1-k) g(\mathbf{z}_2) \end{aligned}$

따라서 $g$ 역시 Convex & Concave 하다.

2. Multiplication

$\gamma \in [0, 1]$ : Affine set $\mathbb{A}_o$ 는 원점을 지나는 Convex set 이므로, 두 원소 $\mathbf{z}, 0 \in \mathbb{A}_o$ 에 대하여,

$\begin{aligned} g(\gamma \mathbf{z}) &= g(\gamma \mathbf{z} + (1-\gamma) 0) \\ &= \gamma g(\mathbf{z}) + (1-\gamma) g(0) \\ &= \gamma g(\mathbf{z}) \end{aligned}$

$\gamma \gt 1$ : 이 경우 $\tfrac{1}{\gamma} \in [0,1]$ 이므로,

$\begin{aligned} g(\mathbf{z}) &= g \left(\tfrac{1}{\gamma} \gamma \mathbf{z} + (1- \tfrac{1}{\gamma}) 0 \right) \\ &= \tfrac{1}{\gamma} g(\gamma \mathbf{z}) + (1-\tfrac{1}{\gamma}) g(0) \\ &= \tfrac{1}{\gamma} g(\gamma \mathbf{z}) \end{aligned}$

$\Longrightarrow ~g(\gamma \mathbf{z}) = \gamma g(\mathbf{z})$

따라서 모든 $\gamma \ge 0$ 에 대하여 $g(\gamma \mathbf{z}) = \gamma g(\mathbf{z})$ 임을 알 수 있다.

3. Additivity

바로 위에서 증명한 Multiplication과, $g$ 가 Convex & Concave하다는 사실을 이용한다.

$\begin{aligned} g(\mathbf{z}_1 + \mathbf{z}_2) &= g(\tfrac{1}{2} 2\mathbf{z}_1 + \tfrac{1}{2} 2 \mathbf{z}_2) \\ &= \tfrac{1}{2} g(2 \mathbf{z}_1) + \tfrac{1}{2} g(2 \mathbf{z}_2) \\ &= g(\mathbf{z}_1) + g(\mathbf{z}_2) \\ \end{aligned}$

위의 3 가지를 모두 증명하였다. 이제 마지막으로, 함수 $g$ 를 Affine map의 형태로 유도해보자. 임의의 원소 $\mathbf{z} \in \mathbb{A}_o \subset \mathbb{R}^n$ 는 표준 베이시스⁵ $\mathbf{e}_i \in \mathbb{R}^n$ 의 선형결합으로 기술할 수 있고,

$\mathbf{z} = z_1 \mathbf{e}_1 + \cdots + z_n \mathbf{e}_n$

위에서 증명한 Multiplication과 Additivity을 이용하면,

$\begin{aligned} g(\mathbf{z}) &= g(z_1 \mathbf{e}_1 + \cdots + z_n \mathbf{e}_n) \\ &=z_1 g(\mathbf{e}_1) + \cdots + z_n g(\mathbf{e}_n) \\ &= \begin{bmatrix} g(\mathbf{e}_1) \cdots g(\mathbf{e}_n) \end{bmatrix} \mathbf{z} \end{aligned}$

따라서 임의의 $\mathbf{x} = \mathbf{z} + \alpha \in \mathbb{A}$ 에 대하여,

$\begin{aligned} f(\mathbf{x}) &= g(\mathbf{x}-\alpha) + f(\alpha) \\ &= \begin{bmatrix} g(\mathbf{e}_1) \cdots g(\mathbf{e}_n) \end{bmatrix} (\mathbf{x} - \alpha) + f(\alpha) \\ &= \begin{bmatrix} g(\mathbf{e}_1) \cdots g(\mathbf{e}_n) \end{bmatrix} \mathbf{x} + f(\alpha) - \begin{bmatrix} g(\mathbf{e}_1) \cdots g(\mathbf{e}_n) \end{bmatrix} \alpha \end{aligned}$

여기서 벡터 $\mathbf{a} = [a_i] \in \mathbb{R}^n$ 와 상수 $b \in \mathbb{R}$ 을 다음과 같이 정의하면,

$\begin{aligned} a_i &= g(\mathbf{e}_i) \\ b &= f(\alpha) - \mathbf{a}^\mathsf{T} \alpha \end{aligned}$

함수 $f$ 는 결국 Affine map의 형태가 된다.

$f(\mathbf{x}) = \mathbf{a}^\mathsf{T} \mathbf{x} + b$

Jesen 부등식

Jensen 부등식

Convex set $\mathbb{S}$ 에서 정의된 Convex function ⁶ $f(\cdot): \mathbb{S} \mapsto \mathbb{R}$ 가 있다. 임의의 $\mathbf{x}_i \in \mathbb{S}$ 및 $\lambda_i \in (0,1)$ 에 대하여, $\lambda_1 + \cdots + \lambda_r = 1$ 라고 할 때, 다음의 부등식이 성립한다. 이를 Jensen 부등식이라고 한다.

$f \left(\sum_{i=1}^r \lambda_i \mathbf{x}_i\right) \le \sum_{i=1}^r \lambda_i f(\mathbf{x}_i)$

Proof.

귀납법 (Induction)으로 쉽게 증명할 수 있다. $n=2$ 인 경우의 Jensen 부등식은 Convex function의 정의에 의해 자명하다. $n=k$ 에 대해서도 다음의 부등식이 성립한다고 가정하자.

$f \left(\sum_{i=1}^k \lambda_i \mathbf{x}_i\right) \le \sum_{i=1}^k \lambda_i f(\mathbf{x}_i)$

이제 $n=k+1$ 에 대해서 식을 전개하면,

$\begin{aligned} f \left( \sum_{i=1}^{k+1} \lambda_i x_i \right) &= f \left( \sum_{i=1}^{k} \lambda_i x_i + \lambda_{k+1} x_{k+1} \right)\\ &= f \left( (1-\lambda_{k+1}) \sum_{i=1}^{k} \frac{\lambda_i}{1-\lambda_{k+1}} x_i + \lambda_{k+1} x_{k+1} \right)\\ &\le (1-\lambda_{k+1}) f \left( \sum_{i=1}^{k} \frac{\lambda_i}{1-\lambda_{k+1}} x_i \right) + \lambda_{k+1} f(x_{k+1}) \end{aligned}$

여기서 $\frac{\lambda_i}{1-\lambda_{k+1}} \overset{\text{let}}{=} \eta_i$ 로 치환하면,

$\sum_{i=1}^{k} \eta_i = \frac{\lambda_1 + \cdots + \lambda_k}{1-\lambda_{k+1}} = \frac{1-\lambda_{k+1}}{1-\lambda_{k+1}} = 1$

이고, $n=k$ 에 대해서 Jensen 부등식이 성립한다고 했으므로,

$\begin{aligned} (1-\lambda_{k+1}) f \left( \sum_{i=1}^{k} \eta_i x_i \right) &\le (1-\lambda_{k+1}) \sum_{i=1}^k \eta_i f(x_i) \\ &= (1-\lambda_{k+1}) \sum_{i=1}^k \frac{\lambda_i}{1-\lambda_{k+1}} f(x_i) \\ &= \sum_{i=1}^k \lambda_i f(x_i) \end{aligned}$

따라서 다음과 같이 증명이 완성된다.

$\begin{aligned} f \left( \sum_{i=1}^{k+1} \lambda_i x_i \right) &\le \sum_{i=1}^k \lambda_i f(x_i) + \lambda_{k+1} f(x_{k+1}) \\ &= \sum_{i=1}^{k+1} \lambda_i f(x_i) \end{aligned}$

Jensen 부등식에서의 등호조건

Jensen 부등식에서 등호가 성립한다면, 다음의 둘 중 하나가 참이다.

$\mathbf{x}_1 = \cdots = \mathbf{x}_r$
함수 $f$ 가 Affine map

Proof.

Jensen 부등식의 등호가 성립한다고 가정하자.

$f \left(\sum_{i=1}^r \lambda_i \mathbf{x}_i\right) = \sum_{i=1}^r \lambda_i f(\mathbf{x}_i)$

$\mathbf{x}_1 = \cdots = \mathbf{x}_r$ 일 때는 등호가 자명하다.
$\mathbf{x}_1 = \cdots = \mathbf{x}_r$ 가 아니라면, Convex set $\mathbb{S}$ 의 모든 원소에 대해 $f$ 는 Convex & Concave 하므로, 따라서 $f$ 는 Affine map 이다.

Strictly convex function의 Jensen 부등식

Jensen 부등식에서 함수 $f$ 가 Strictly convex function 이라면,

$\mathbf{x}_1 = \cdots = \mathbf{x}_r ~\Longleftrightarrow~ f \left(\sum_{i=1}^r \lambda_i \mathbf{x}_i\right) = \sum_{i=1}^r \lambda_i f(\mathbf{x}_i)$

Proof.

(1) $\Rightarrow$ 자명하다

(2) $\Leftarrow$ Jensen 부등식에서 등호가 성립한다면, $\mathbf{x}_1 = \cdots = \mathbf{x}_r$ 거나 $f$ 가 Affine map 이어야 한다. 그런데 가정에서 $f$ 는 Strictly convex 하므로, 따라서 $\mathbf{x}_1 = \cdots = \mathbf{x}_r$ 인 경우밖에 없다.

확률변수의 Jensen 부등식

Convex function $f(\cdot): \mathbb{S} \mapsto \mathbb{R}$ 과 확률변수 $X$ 에 대하여 다음의 부등식이 성립한다.

$f \left( \mathbf{E}[X] \right) \le \mathbf{E} \left[ f(X) \right]$

만약 $f$ 가 Strictly convex function 이라면,

$f \left( \mathbf{E}[X] \right) = \mathbf{E} \left[ f(X) \right] \Longleftrightarrow X=Const$

이산확률변수의 Jensen 부등식은 자명하다. 연속확률변수인 경우의 증명은 생략한다. 대신, 확률변수의 Jensen 부등식을 직관적으로 이해해보자. 아래 차트는 Convex function $\varphi$ 로 인해, 확률변수 $X$ 의 분포가 $\varphi (X)$ 로 어떻게 mapping 되는 지를 보여준다.

(출처: 위키피디아)

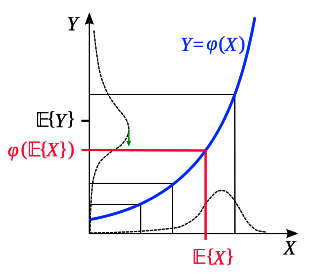
원래의 $X$ 의 분포(예시)는 왼쪽으로 꼬리가 길게 늘어져있고, 이에따라 $X$ 의 기대값 $\mathbf{E}[X]$ 은 다소 왼쪽에 위치하게 된다. 하지만 Convex function의 독특한 형태로 인해 $X$ 분포의 오른쪽 부분이 확장(Stretching-out) 변환되면서, 확률변수 $Y=\varphi(X)$ 의 분포 상단이 점차 늘어지는 모양이 되었다. 결과적으로 $Y$ 의 기대값 $\mathbf{E}[Y]$ 을 위로 밀어올리게 되면서, $\varphi(\mathbf{E}[X]) \le \mathbf{E}[Y] = \mathbf{E}[\varphi(X)]$ 의 관계를 도출하게 되는데, 이것이 바로 확률변수의 Jensen 부등식인 것이다.

Affine transformation, Affine function 이라고도 한다. 여기를 참고. ↩
선형변환, Linear transformation, Linear function 이라고도 한다. 여기를 참고. ↩
평행이동 변환을 의미한다. 여기를 참고. ↩
이처럼 어떤 집합(그림에서는 $\{ \mathbf{x}_1, \mathbf{x}_2 \}$ )을 포함하고 있는 최소한의 Affine set과 Convex set을 각각 Affine hull, Convex hull 이라고 부른다. ↩
$i$ 번째 항목만 1 이고 나머지는 0인 벡터를 말한다. 기저 (Standard basis)라고도 한다. ↩
가 Concave function 인 경우에는 부등호의 방향이 반대가 된다. $f \left(\sum_{i=1}^n \lambda_i x_i\right) \ge \sum_{i=1}^n \lambda_i f(x_i)$ ↩

Written on July 29th, 2018 by quanty

Feel free to share!

Affinity와 Convexity

Affinity

Affine combination

Affine set

Affine map

Convexity

Convex combination

Convex set

Convex function

Strictly convex function

Convex + Concave = Affine map

Jesen 부등식

Jensen 부등식

Jensen 부등식에서의 등호조건

Strictly convex function의 Jensen 부등식

확률변수의 Jensen 부등식

관련 포스트

정보이론의 기초

K-means clustering