K-means clustering

# Machine learning

데이터에 대한 사전정보가 전혀 없는 상태에서, 해당 데이터들을 몇 개의 그룹으로 나누고 싶을 때가 있다. 이를 클러스터링 문제라고 한다. 머신러닝에서 클러스터링은 전형적인 비지도학습 (Unsupervised learning)에 해당한다. 그 중에서 특히 K-mean clustering은 단지 거리정보만을 이용하여 클러스터링을 수행하는 단순한 알고리즘을 쓰기 때문에, 구현하기가 상대적으로 수월하다.

Iteration에 따른 클러스터 추정의 수렴 iterations

개요
알고리즘
알고리즘의 유도
- Assignment
- Update
예제
한계
EM 알고리즘

개요

$n$ 개의 입력데이터 $\mathbf{X} = (\mathbf{x}_1 \cdots \mathbf{x}_n)$ , $\mathbf{x}_i \in \mathbb{R}^d$ 를 $k$ 개의 클러스터 $\mathbf{S} = \{ S_1, \cdots, S_k \}$ 에 배정하려고 한다. 이때 클러스터의 갯수 $k$ ( $\le n$ )는 미리 정해져 있다고 가정한다.

이 문제를 모델링 해보자. 우선 임의의 클러스터 $\mathbf{S}$ 에 대해서, 클러스터 $j$ 의 왜곡도 (Distortion)¹ $\mathcal{D}_j$ 를 정의하고,

$\mathcal{D}_j \equiv \sum_{\mathbf{x} \in S_j} \Vert \mathbf{x} - \boldsymbol{\mu}_j \Vert^2$

총 왜곡도 (Total distortion) ² $\mathcal{J}_\mathbf{S}$ 를 다음과 같이 설정하자.

$\mathcal{J}_\mathbf{S} = \sum_{j=1}^k \mathcal{D}_j = \sum^k_{j=1} \sum_{\mathbf{x} \in S_j} \Vert \mathbf{x} - \boldsymbol{\mu}_j \Vert^2$

여기서 $\boldsymbol{\mu} = \{ \boldsymbol{\mu}_1, \cdots, \boldsymbol{\mu}_k \}$ 는 각 클러스터의 Centroid(중심점)을 의미한다. 즉 총 왜곡도는 각 클러스터에 속한 데이터들이 해당 Centroid로부터 얼마나 떨어져 있는지를 나타내는 지표이다.

K-means clustering은 총 왜곡도를 최소화하는 클러스터 $\hat{\mathbf{S}}$ 를 찾는 최적화 알고리즘³이다. 즉,

$\hat{\mathbf{S}} = \underset{\mathbf{S}}{\arg \min} ~\mathcal{J}_\mathbf{S} = \underset{\mathbf{S}}{\arg \min} \sum^k_{j=1} \sum_{\mathbf{x} \in S_j} \Vert \mathbf{x} - \boldsymbol{\mu}_j \Vert^2$

이 문제는 대수적으로 명쾌하게 풀리지 않는다. 위의 총 왜곡도를 최소화하기 위해서는 우선 Centroid $\boldsymbol{\mu}$ 에 대한 정보를 알고 있어야 하는데, 이 값들은 클러스터 $\mathbf{S}$ 가 정해져 있어야 알 수 있는 값들이기 때문이다. 따라서 K-means clustering은 수치적인 접근방법을 쓴다. 반복적인(iterative) 절차를 통해 $\mathbf{S}$ 와 $\boldsymbol{\mu}$ 를 번갈아가며 추정하는 과정에서 최적 클러스터 $\hat{\mathbf{S}}$ 로 수렴해 나간다. K-means clustering은 데이터에 대한 사전정보(즉 레이블)가 없는 상태로 데이터 간의 특정 패턴을 추정한다는 측면에서, 머신러닝의 비지도 학습 (Unsupervised learning)에 해당한다.

K-NN 알고리즘

K-NN (K-Nearest Neighbors)과 K-mean는 전혀 다른 알고리즘이다. K-NN은 머신러닝의 지도학습 (Supervised learning)에 속하며, 특정 데이터 주위에 있는 데이터들을 통해 해당 데이터의 특성을 파악하는 단순한 기법이다.

K-NN Classification: 주위의 $k$ 개 데이터 중 (다수결의 원칙에 의해) 대다수가 속해있는 Class에 해당 데이터를 할당한다. 만약 $k=1$ 이라면, 가장 근접한 데이터가 속해있는 Class에 할당된다.

K-NN Regression: 주위 $k$ 개 데이터의 평균값을 해당 데이터에 할당한다.

알고리즘

K-means clustering 문제의 수치적인 해결을 위해, 위에서 정의된 왜곡도 $\mathcal{D}_j$ 를 다음과 같이 풀어쓰자.

$\mathcal{D}_j = \sum_{\mathbf{x} \in S_j} \Vert \mathbf{x} - \boldsymbol{\mu}_j \Vert^2 = \sum^n_{i=1} r_{ij} \Vert \mathbf{x}_i - \boldsymbol{\mu}_j \Vert^2$

여기서 $\mathbf{r} = \{ r_{ij} \}$ 는 각 데이터가 어떤 클러스터에 속해있는 지를 나타내주는 이산변수(Discrete variable) $r_{ij}$ 들의 집합이며, 다음과 같이 정의된다.

$r_{ij} \equiv \begin{cases} 1 & \text{if} ~~\mathbf{x}_i \in S_j \\ 0 & \text{otherwise} \end{cases}$

예를들어 $\mathbf{x}_1 \in S_2$ , $\mathbf{x}_2 \in S_2$ , $\mathbf{x}_3 \in S_1$ 이라면,

$\begin{pmatrix} r_{11}=0 \\ r_{12}=1 \end{pmatrix}, ~ \begin{pmatrix} r_{21}=0 \\ r_{22}=1 \end{pmatrix}, ~ \begin{pmatrix} r_{31}=1 \\ r_{32}=0 \end{pmatrix}$

이 된다. 앞으로 $\mathbf{r}$ 을 클러스터라고 부를 것이다. 이제 총 왜곡도는 다음과 같이 $\mathcal{J}_\mathbf{r}$ 로 변경되며, 원래의 클러스터링 문제는 결국 최적의 클러스터 $\mathbf{r}$ 을 찾는 문제로 귀결된다.

$\min_{\mathbf{S}} \mathcal{J}_\mathbf{S} = \min_{\mathbf{r}} \mathcal{J}_\mathbf{r}$

$\mathcal{J}_\mathbf{r} = \sum^n_{i=1} \sum^k_{j=1} r_{ij} \Vert \mathbf{x}_i - \boldsymbol{\mu}_j \Vert^2$

K-means clustering은 Centroid $\boldsymbol{\mu}$ 의 추정값이 수렴할 때까지 다음의 Assignment 와 Update 를 반복하여 수행한다.

Centroid 초기화
- Centroid의 추정값 $\hat{\boldsymbol{\mu}}$ 를 임의의 값 $\hat{\boldsymbol{\mu}}(0) = \{ \hat{\boldsymbol{\mu}}_1(0), \cdots, \hat{\boldsymbol{\mu}}_k(0) \}$ 으로 초기화
- 초기화 기법: 무작위 분할법(Random partition)⁴, Forgy⁵ 등

Assignment
- 이전 단계에서 추정한 Centroid $\hat{\boldsymbol{\mu}}$ 을 이용하여 클러스터 $\hat{\mathbf{r}}$ 을 추정하는 단계
- 각각의 데이터에 가장 가까운 클러스터를 할당
Update
- 이전 단계에서 추정한 클러스터 $\hat{\mathbf{r}}$ 을 이용하여 Centroid $\hat{\boldsymbol{\mu}}$ 을 업데이트하는 단계
- $\hat{\boldsymbol{\mu}} =$ 각각의 클러스터에 속한 데이터들의 샘플 평균값
종료
- $\hat{\boldsymbol{\mu}}$ 가 수렴하면(즉 $\hat{\mathbf{r}}$ 의 변동이 없으면) 알고리즘을 종료

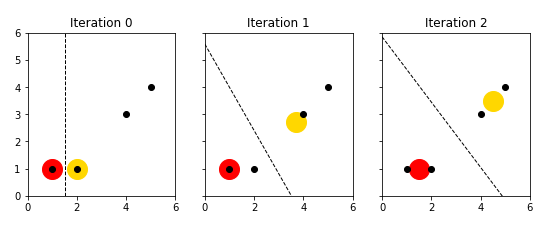
다음은 iteration이 진행됨에 따라 클러스터가 어떻게 추정되는 지를 도식화한 그림이다. $d=2$ (즉 2차원 데이터), $k=3$ (3개의 클러스터로 구분) 에 대하여, 3개의 Centroid ( $\color{red}{+}$ , $\color{gold}{\times}$ , $\color{blue}{\circ}$ )가 어떻게 update 되는 지를 확인할 수 있다.

Convergence of K-means K-means convergence.gif

(출처: 위키피디아)

알고리즘의 유도

Assignment

직전 단계에서 Centroid 추정값 $\hat{\boldsymbol{\mu}}(t) = \{ \hat{\boldsymbol{\mu}}_1 (t), \cdots, \hat{\boldsymbol{\mu}}_k (t) \}$ 가 주어졌다면, 총 왜곡도는 다음과 같이 분해된다.

$\mathcal{J}_\mathbf{r} = \sum^k_{j=1} r_{1j} {\underbrace{\Vert \mathbf{x}_1 -\hat{\boldsymbol{\mu}}_j(t) \Vert}_{\text{minimize}}}^2 + \cdots + \sum^k_{j=1} r_{nj} {\underbrace{\Vert \mathbf{x}_n -\hat{\boldsymbol{\mu}}_j(t) \Vert}_{\text{minimize}}}^2$

이 때 $r_{ij} \ge 0$ 이고 $\Vert \cdot \Vert \ge 0$ 이다. 그러므로 $\mathcal{J}_\mathbf{r}$ 을 $\mathbf{r}$ 에 대해서 최소화 한다는 얘기는, 각각의 데이터 $\mathbf{x}_i$ 에 대해 $\Vert \mathbf{x}_i -\hat{\boldsymbol{\mu}}_j(t) \Vert$ 를 최소화 한다는 말과 동일하고, 이는 각 데이터를 가장 가까운 클러스터에 단순히 할당한다는 의미가 된다. 따라서 주어진 Centroid $\hat{\boldsymbol{\mu}}(t)$ 에 대해, 클러스터 $\hat{\mathbf{r}}(t) = \{ \hat{r}_{ij}(t) \}$ 는 다음과 같이 정해진다.

$\hat{r}_{ij} (t) = \begin{cases} 1 & \text{if} ~~j = \underset{\ell}{\arg \min} \Vert \mathbf{x}_i - \hat{\boldsymbol{\mu}}_\ell (t) \Vert \\ 0 & \text{otherwise} \end{cases}$

Update

이전 단계에서 추정된 클러스터 $\hat{\mathbf{r}}(t) = \{ \hat{r}_{ij}(t) \}$ 가 주어진 상태에서, 총 왜곡도 $\mathcal{J}_\mathbf{r}$ 를 최소화 해보자.

$\displaystyle \frac{\partial \mathcal{J}_\mathbf{r}}{\partial \boldsymbol{\mu}} = \left[ \frac{\partial \mathcal{J}_\mathbf{r}}{\partial \boldsymbol{\mu}_1} \cdots \frac{\partial \mathcal{J}_\mathbf{r}}{\partial \boldsymbol{\mu}_k} \right]^\mathsf{T} = 0$ 에서,

$\begin{aligned} \frac{\partial \mathcal{J}_\mathbf{r}}{\partial \boldsymbol{\mu}_j} \bigg|_{\hat{\boldsymbol{\mu}}_j} &= \frac{\partial}{\partial \boldsymbol{\mu}_j} \left[ \sum^n_{i=1} \sum^k_{j=1} \hat{r}_{ij}(t) \Vert \mathbf{x}_i - \boldsymbol{\mu}_j \Vert^2 \right]_{\hat{\boldsymbol{\mu}}_j} \\ &= \frac{\partial}{\partial \boldsymbol{\mu}_j} \left[ \sum^n_{i=1} \hat{r}_{ij}(t) ( \mathbf{x}_i - \boldsymbol{\mu}_j )^T ( \mathbf{x}_i - \boldsymbol{\mu}_j ) \right] _{\hat{\boldsymbol{\mu}}_j}\\ &= -2 \sum^n_{i=1} \hat{r}_{ij}(t) ( \mathbf{x}_i - \hat{\boldsymbol{\mu}}_j ) \\ &= -2 \left[ \sum^n_{i=1} \hat{r}_{ij}(t) ~\mathbf{x}_i - \left( \sum^n_{i=1} \hat{r}_{ij}(t) \right) \hat{\boldsymbol{\mu}}_j \right] \\ &= 0 \end{aligned}$

$\therefore \hat{\boldsymbol{\mu}}_j (t+1) = \frac{\sum^n_{i=1} \hat{r}_{ij}(t) ~\mathbf{x}_i}{\sum^n_{i=1} \hat{r}_{ij}(t)}$

따라서 Centroid $\hat{\boldsymbol{\mu}}(t+1) = \{ \hat{\boldsymbol{\mu}}_1(t+1), \cdots, \hat{\boldsymbol{\mu}}_k(t+1) \}$ 는 각각의 클러스터에 속한 데이터들의 샘플 평균값으로 계산된다. 이 알고리즘을 K-means 라고 부르는 이유이기도 하다.

예제

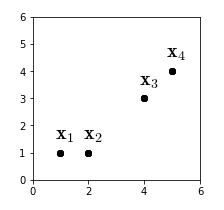
다음과 같이 4개의 데이터⁶가 주어져 있다. 이 데이터들을 2개의 클러스터에 할당해보자. 즉 n=4, d=2, k=2 가 된다. 직관적으로 봤을 때는 $\{ \mathbf{x}_1, \mathbf{x}_2 \}$ 와 $\{ \mathbf{x}_3, \mathbf{x}_4 \}$ 으로 클러스터링이 될 것 같다.

데이터	$\mathbf{x}_1$	$\mathbf{x}_2$	$\mathbf{x}_3$	$\mathbf{x}_4$
좌표	(1, 1)	(2, 1)	(4, 3)	(5, 4)

Iteration 0 (t=0)

Centroid 초기화: 데이터 중 임의로 두 개를 선택한다.

$\begin{aligned} \hat{\boldsymbol{\mu}}_1(0) &= \mathbf{x}_1 = (1,1) \\ \hat{\boldsymbol{\mu}}_2(0) &= \mathbf{x}_2 = (2,1) \end{aligned}$

Assignment: 각 데이터에서 Centroid 까지의 유클리드 거리를 계산한다.

Centroid와의 거리	$\mathbf{x}_1$	$\mathbf{x}_2$	$\mathbf{x}_3$	$\mathbf{x}_4$
$\hat{\boldsymbol{\mu}}_1(0)$	0.0	1.0	3.6	5.0
$\hat{\boldsymbol{\mu}}_2(0)$	1.0	0.0	2.8	4.2

예를들어 $\mathbf{x}_4$ 와 $\hat{\boldsymbol{\mu}}_2(0)$ 간의 거리는 $\sqrt{(5-2)^2 + (4-1)^2}=4.2$ 로 계산된다. 이 예제에서 모든 거리는 소숫점 둘째자리에서 반올림 되었다. 이제 각 데이터별로 짧은 거리의 Centroid를 선택하면, 다음과 같이 클러스터 추정치 $\hat{\mathbf{r}}(0) = \{ \hat{r}_{ij}(0) \}$ 를 얻게 된다.

	$\mathbf{x}_1$	$\mathbf{x}_2$	$\mathbf{x}_3$	$\mathbf{x}_4$
$S_1$	$\hat{r}_{11}(0)=1$	$\hat{r}_{21}(0)=0$	$\hat{r}_{31}(0)=0$	$\hat{r}_{41}(0)=0$
$S_2$	$\hat{r}_{12}(0)=0$	$\hat{r}_{22}(0)=1$	$\hat{r}_{32}(0)=1$	$\hat{r}_{42}(0)=1$

즉 $\{ \mathbf{x}_1 \}$ 과 $\{ \mathbf{x}_2, \mathbf{x}_3, \mathbf{x}_4 \}$ 로 클러스터링이 된다.

Iteration 1 (t=1)

Update: 이전 단계에서 추정한 클러스터를 기준으로 Centroid를 재계산한다.

$\begin{aligned} \hat{\boldsymbol{\mu}}_1(1) &= \mathbf{x}_1 = (1,1) \\ \hat{\boldsymbol{\mu}}_2(1) &= \frac{\mathbf{x}_2 + \mathbf{x}_3 + \mathbf{x}_4}{3} = (3.7, ~2.7) \end{aligned}$

Assignment: 재계산된 Centroid를 통해 클러스터를 재추정한다.

Centroid와의 거리	$\mathbf{x}_1$	$\mathbf{x}_2$	$\mathbf{x}_3$	$\mathbf{x}_4$
$\hat{\boldsymbol{\mu}}_1(1)$	0.0	1.0	3.6	5.0
$\hat{\boldsymbol{\mu}}_2(1)$	3.1	2.4	0.5	1.9

	$\mathbf{x}_1$	$\mathbf{x}_2$	$\mathbf{x}_3$	$\mathbf{x}_4$
$S_1$	$\hat{r}_{11}(1)=1$	$\hat{r}_{21}(1)=1$	$\hat{r}_{31}(1)=0$	$\hat{r}_{41}(1)=0$
$S_2$	$\hat{r}_{12}(1)=0$	$\hat{r}_{22}(1)=0$	$\hat{r}_{32}(1)=1$	$\hat{r}_{42}(1)=1$

$\{ \mathbf{x}_1 \}$ 의 클러스터에 $\mathbf{x}_2$ 가 신규 편입된 것을 알 수 있다.

Iteration 2 (t=2)

Update: 이전 단계에서 추정한 클러스터를 기준으로 Centroid를 재계산한다.

$\begin{aligned} \hat{\boldsymbol{\mu}}_1(2) &= \frac{\mathbf{x}_1 + \mathbf{x}_2}{2} = (1.5,~1) \\ \hat{\boldsymbol{\mu}}_2(2) &= \frac{\mathbf{x}_3 + \mathbf{x}_4}{2} = (4.5, ~3.5) \end{aligned}$

Assignment: 재계산된 Centroid를 통해 클러스터를 재추정한다.

Centroid와의 거리	$\mathbf{x}_1$	$\mathbf{x}_2$	$\mathbf{x}_3$	$\mathbf{x}_4$
$\hat{\boldsymbol{\mu}}_1(2)$	0.5	0.5	3.2	4.6
$\hat{\boldsymbol{\mu}}_2(2)$	4.3	3.5	0.7	0.7

	$\mathbf{x}_1$	$\mathbf{x}_2$	$\mathbf{x}_3$	$\mathbf{x}_4$
$S_1$	$\hat{r}_{11}(2)=1$	$\hat{r}_{21}(2)=1$	$\hat{r}_{31}(2)=0$	$\hat{r}_{41}(2)=0$
$S_2$	$\hat{r}_{12}(2)=0$	$\hat{r}_{22}(2)=0$	$\hat{r}_{32}(2)=1$	$\hat{r}_{42}(2)=1$

Iteration에 따른 클러스터 추정의 수렴 iterations

클러스터에 변화가 없으므로, iteration 2에서 알고리즘을 종료한다. 결국 직관대로 클러스터는 $\{ \mathbf{x}_1, \mathbf{x}_2 \}$ 와 $\{ \mathbf{x}_3, \mathbf{x}_4 \}$ 로 묶이게 되었다. 물론 데이터의 차원이 커지게 되면 (즉 d가 커지게 되면) 직관적인 추정 자체가 불가능해 지는 경우가 많아진다.

한계

K-means clustering은, 알고리즘이 단순한 만큼 여러가지 한계점을 지니고 있다.

클러스터의 갯수 $k$ 를 미리 지정해야 한다: $k$ 값에 따라 결과값은 천차만별일 수 있기 때문에, $k$ 를 모른다는 것은 알고리즘의 결정적인 한계라고 볼 수 있다. Elbow method 등, 이를 타개하기 위한 여러가지 방법론이 있다.
전역 최적해(Global optima)을 보장하지 않는다: 최적 클러스터가 지역 최적해(Local optima)에 수렴할 가능성이 있다. 따라서 여러가지 초기값으로 테스트해 본 후, 총 왜곡도가 가장 낮은 결과를 수용하는 등의 방식으로 한계를 완화한다.
Centroid 초기화가 알고리즘 성능에 영향을 줄 수 있다: 잘못된 초기화는 수많은 iteration을 수반할 수 있기 때문에, 알고리즘의 성능에 악영향을 미칠 수 있다. 적절한 Centroid 초기값을 결정하는 여러가지 알고리즘이 있는데, 가장 유명한 것이 K-means++ 이다.
Outlier에 예민하다: Centroid를 각 클러스터 데이터들의 샘플평균으로 계산하기 때문에, 클러스터에 outlier가 포함되면 Centroid가 크게 왜곡될 수 있다.
다양한 모양의 클러스터에 취약하다: 유클리드 거리(Euclidean distance)로 총 왜곡도를 산출하기 때문에, 각 Centroid로부터 구형(Spherical)의 클러스터가 만들어진다. 따라서 도넛형, 사각형, 럭비공형 등 다양한 모양의 클러스터를 인식하기에는 적합하지 않다.
Hard clustering: 만약 어떤 한 데이터가 여러 개의 Centroid들로부터 같은 위치에 존재한다면? 참 애매할 것이다. K-mean는 어떤 클러스터에 속할지 안속할지를 이분법적으로 판단하는 데, 이를 Hard clustering 이라고 부른다. ⁷

EM 알고리즘

K-means clustering의 Assignment-Update 프로세스를 일반화시키면 EM (Expectation-Maximization) 알고리즘이 된다. EM 알고리즘은 다른 포스트에서 자세히 소개할 예정이다.

비용함수(Cost function) 이라고도 한다. ↩
WCSS(Within-Cluster Sum-of-Squares) 또는 Inertia 라고 부르기도 한다. ↩
Lloyd 알고리즘이라고도 한다. ↩
가장 많이 쓰이는 방법으로, 데이터들을 임의의 클러스터에 우선 할당한 후, 해당 클러스터의 평균값으로 Centroid를 초기화한다. ↩
데이터 집합에서 선택한 임의의 $k$ 개 데이터를 Centroid 초기값으로 본다. ↩
이 예제는 여기의 데이터를 참고로 하였다. ↩
Hard clustering과는 달리, 어떤 클러스터에 속할 확률값을 계산하여 클러스터링을 하는 방법도 존재하는데, 이를 Soft clustering 이라고 한다. 대표적으로는 GMM이 있다. ↩

Written on July 15th, 2018 by quanty

Feel free to share!

K-means clustering

개요

알고리즘

알고리즘의 유도

Assignment

Update

예제

한계

EM 알고리즘

관련 포스트

정보이론의 기초

Affinity와 Convexity